Предмет: Алгебра,
автор: FuoLeTaBoeKuBu
Пожалуйста помгите :-)
Докажите, что значение выражения не зависит от значения входящей
в него переменной: 1)3x²-27/4x²+2×(6x+1/x-3+6x-1/x+3) ;
2)3/2a-3-8a-18a/4a²+9×(2a/4a²-12a+9-3/4a²-9)
Приложения:
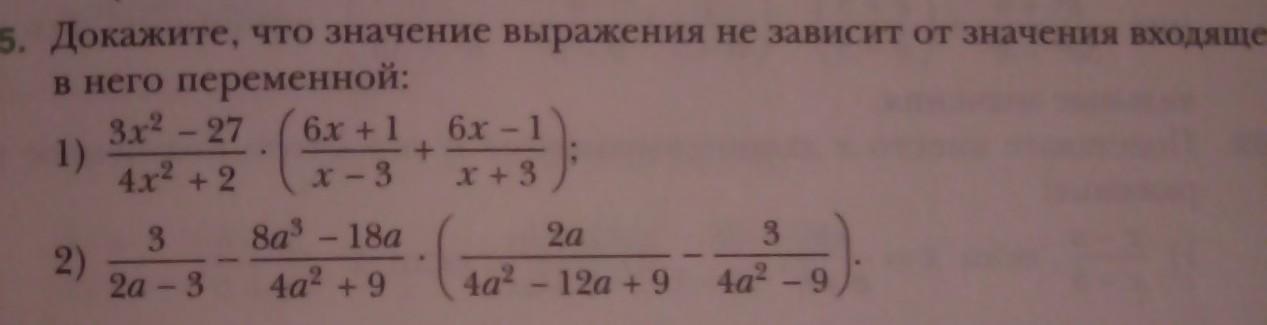
Ответы
Автор ответа:
4
1)
2)
Похожие вопросы
Предмет: Русский язык,
автор: lira0804
Предмет: Другие предметы,
автор: chpunsara
Предмет: Математика,
автор: rauka1982
Предмет: Математика,
автор: полька170
Предмет: Математика,
автор: losos12