Предмет: Математика,
автор: nezoxxxs
Найти косинус угла между диагоналями параллелограмма, построенного на векторах а(3;2) та b(1;-2) с точностью до 0,01.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
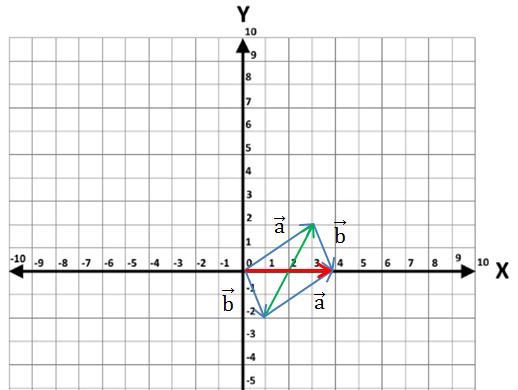
Векторы d1 и d2, направленные по диагоналям параллелограмма определяем как разность векторов a и b (см. рисунок: зелёный вектор) и как сумма векторов a и b (см. рисунок: красный вектор):
d1 = a - b = (3; 2) - (1; -2) = (3-1; 2-(-2)) = (2; 4),
d2 = a + b = (3; 2) + (1; -2) = (3+1; 2+(-2)) = (4; 0).
Скалярное произведение векторов d1(x₁; y₁) и d2(x₂; y₂) можно определить по формулам:
d1·d2=x₁·x₂+y₁·y₂ и d1·d2=|d1|·|d2|·cosα,
где |d1| и |d2| длины векторов, соответственно, d1 и d2, α - угол между векторами d1 и d2.
Определяем длины векторов d1 и d2:
Скалярное произведение векторов d1(x₁; y₁) и d2(x₂; y₂) определяем через координаты:
d1·d2=2·4+4·0=8.
Тогда косинус угла между векторами d1 и d2 равен:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nikolay2005
Предмет: Информатика,
автор: nikitka34761
Предмет: Другие предметы,
автор: mszhemaylova
Предмет: Литература,
автор: smirnowadana201
Предмет: Алгебра,
автор: мила285