Question

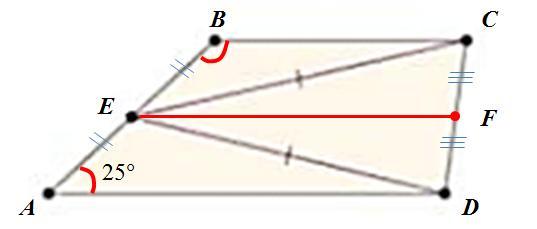
Середина боковой стороны трапеции равноудалена от двух вершин противоположной боковой стороны. Один из углов трапеции равен 25°. Найдите углы трапеции. Прошу помогите

Answer 1

Ответ:

∠A=25°, ∠B=155°, ∠С=∠D=90°

Объяснение:

Дано (см. рисунок):

  Трапеция ABCD, о есть AD||BC

  ∠А = 25°

  AE=EB

  EC=ED  

Найти: ∠B, ∠C, ∠D.

Решение. В трапеции основания параллельны, то есть: AD||BC и поэтому

∠В = 180°–∠А = 180°–25° = 155°.  

Из середины стороны АВ, то есть из точки E, проведём среднюю линию EF. Так как в треугольнике DEC: EC=ED, то треугольник DEC – равнобедренный, и поэтому по свойству равнобедренных треугольников средняя линия трапеции EF и медиана и биссектриса и высота в треугольнике DEC.

Далее, так как EF высота, то ∠EFС=∠EFD=90°. Но тогда из-за EF||AD||BC получаем, что ∠EFС=∠С=∠D=90°.