Предмет: Геометрия,
автор: tlzukova221105
Острый угол ромба равен 45°, а его площадь равна 18√2. Найдите сторону ромба.
Ответы
Автор ответа:
1
Ответ:
Сторона ромба равна 6 см.
Объяснение:
Ромб - это параллелограмм, у которого все стороны равны.
Площадь ромба через его сторону и угол можно найти по формуле:
Выразим сторону ромба.
Значение синуса 45° найдем из таблиц значений тригонометрических функций:
Подставим данные в выражение стороны ромба:
Сторона ромба равна 6 см.
Приложения:
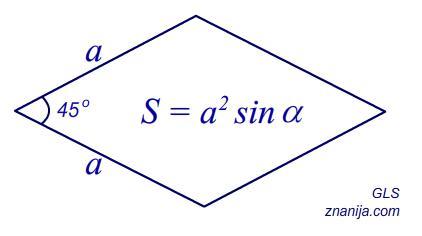
Похожие вопросы
Предмет: Геометрия,
автор: IvaNikas
Предмет: Русский язык,
автор: makshka12
Предмет: Математика,
автор: Anjelina2006
Предмет: Математика,
автор: балдиеваженнет
Предмет: Биология,
автор: directionerforever28