Предмет: Геометрия,
автор: gerhat228
в равнобедренном треугольнике длина основания 23 см проведена биссектриса угла ABC используя второй признак равенства треугольников Докажите что отрезок BD является медианой и определи длину отрезка AD
Приложения:
Ответы
Автор ответа:
9
Ответ:
11,5 см
Объяснение:
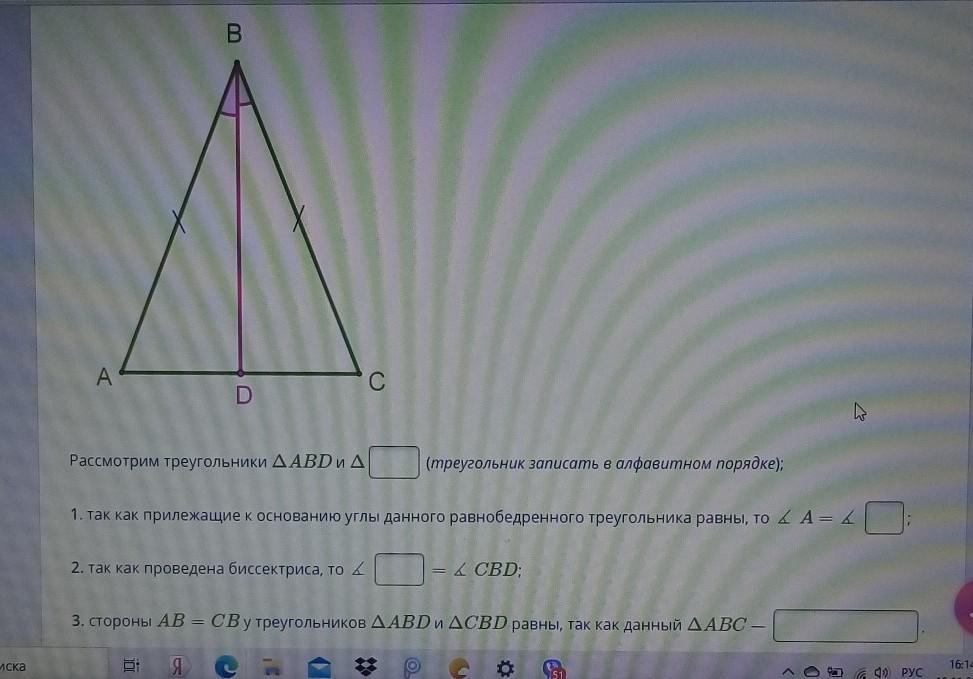
Рассмотрим ΔABD и ΔBCD:
1) так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∠А = ∠С;
2) так как проведена биссектриса, то ∠ABD = ∠CBD;
3) стороны АВ и СВ у треугольников ABD и BCD равны, так как данный ΔАВС - равнобедренный, следовательно
ΔABD = ΔBCD по второму признаку равенства треугольников.
В равных треугольниках против равных углов лежат равные стороны, значит AD = DC.
Так как D - середина АС, то BD является медианой.
AD = AC/2 = 23/2 = 11,5 см
Похожие вопросы
Предмет: Русский язык,
автор: АлександрМинтяков
Предмет: Русский язык,
автор: klkteva05101969
Предмет: Русский язык,
автор: Витраж007
Предмет: Математика,
автор: nastyaegor2008
Предмет: Геометрия,
автор: F1fristaylo