Предмет: Математика,
автор: rewwge222
Надо решить показательные неравенства, даю 45 баллов
Приложения:
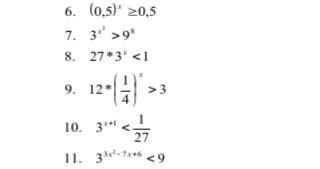
Ответы
Автор ответа:
1
Ответ:
Ответ: х принадлежит (-беск;0)U(2;+беск).
Ответ: х принадлежит (1;4/3).
Похожие вопросы
Предмет: Математика,
автор: yeseny
Предмет: Русский язык,
автор: karapetsmbatyan
Предмет: Математика,
автор: rstamovaaliska
Предмет: Математика,
автор: juliya105