Question

Основанием прямой призмы является ромб, диагонали которого равны 7см и 12  см. Большее диагональное сечение призмы равно 72см2. Вычисли объём призмы.

Объём призмы равен
см3.
​

Answer 1

Ответ:

$V = 252$ см³

Объяснение:

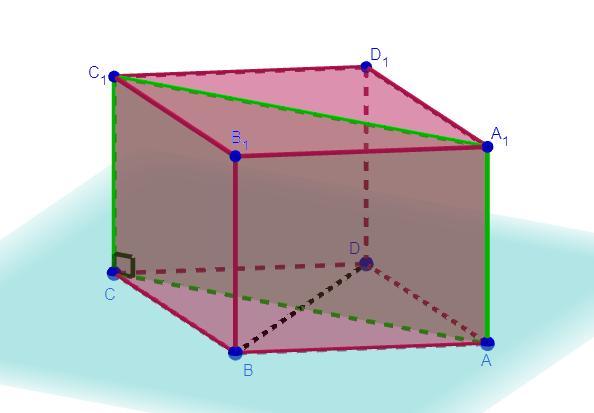
Дано: $ABCDA_{1}B_{1}C_{1}D_{1} -$ прямая призма, AB = BC = CD = DA (ABCD - ромб),

AC = 12 см, BD = 7 см,  $S_{AA_{1}C_{1}C} = 72$ см²

Найти: $V$ - ?

Решение: По формуле площади ромба: $S_{ABCD} = 0,5 * AC * BD = 0,5 * 12 * 7 = 6 * 7 = 42$ см².

Так как по условию $ABCDA_{1}B_{1}C_{1}D_{1} -$ прямая призма, то отрезок $CC_{1} -$ высота призмы и по свойствам прямой призмы её диагональным сечением является прямоугольник. Тогда $AA_{1}C_{1}C -$ прямоугольник. По формуле площади прямоугольника:

$S_{AA_{1}C_{1}C} = CC_{1} * AC \Longrightarrow CC_{1} = \dfrac{S_{AA_{1}C_{1}C}}{AC} = \dfrac{72}{12} = 6$.

По формуле объема призмы:

$V = CC_{1} * S_{ABCD} = 6 * 42 = 252$ см³.