Question

Задача: діагональ правильної чотирикутної призми рівна 4см, сторона основи 2см.

Знайти площу повної поверхні призми.

Answer 1

Ответ:

8+16√2 см²

Объяснение:

Дано:

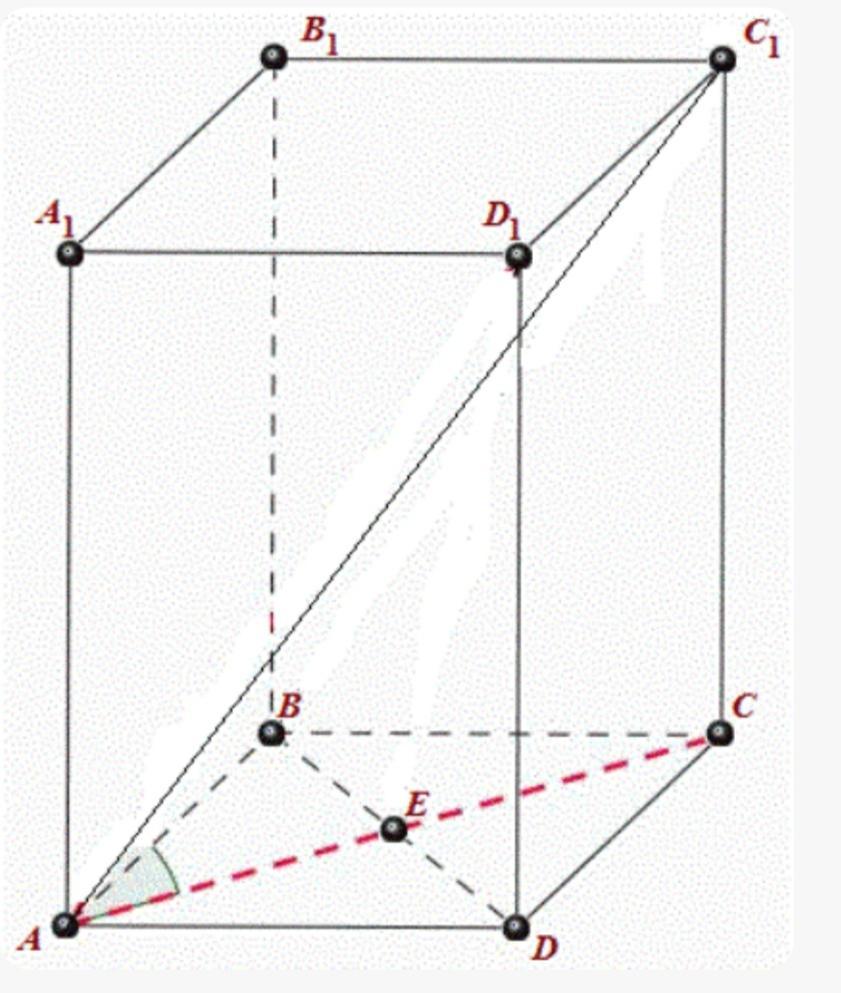
АВСDA1B1C1D1 призма.

АВСD- квадрат.

АС1=4см диагональ призмы.

АВ=ВС=СD=AD=2см

Sпол=?

Решение

Sпол=2Sосн+Sбок

Sосн=АВ²=2²=4 см² площадь квадрата.

АС- диагональ квадрата.

АС=АВ√2=2√2 см диагональ квадрата.

∆АС1С- прямоугольный.

АС1- гипотенуза.

АС и СС1 - катеты.

По теореме Пифагора найдем СС1

СС1=√(АС1²-АС²)=√(4²-(2√2)²)=√(16-8)=√8=

=2√2 см высота призмы.

Формула нахождения площади боковой поверхности призмы

Sбок=Росн.*h, где Росн.-периметр основания (квадрата); h=CC1.

Sбок=4*АВ*СС1=4*2*2√2=16√2 см² площадь боковой поверхности призмы.

Sпол.=2*Sосн.+Sбок=2*4+16√2=8+16√2 см² площадь полной поверхности призмы.