Question

Стороны параллелограмма равны 6 см и 10 см, а один из его углов равна 60°. Найдите длину большей диагонали параллелограмма

Answer 1

Нужно знать:

1) у параллелограмма противоположные стороны равны;

2) cos(180° - α) = -cosα;

3) cos60° = 1/2.

Поэтому:

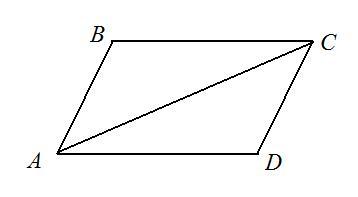
См. рисунок.

Пусть дан параллелограмм АВСD. АВ = 6 см, ВС = 10 см, ∠А = 60°.

Найдем длину большей диагонали.

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, т.е. ∠А + ∠В = 180°, тогда ∠В = 180° - ∠А = 180° - 60° = 120°. Значит, диагональ АС - большая, т.к. лежит против большего ∠В.

По теореме косинусов АС² = АВ² + ВС² - 2 · АВ · ВС · cosB =

= 6² + 10² - 2 · 6 · 10 · cos120° = 36 + 100 - 2 · 6 · 10 · (-cos60°) =

= 136 + 120 · 1/2 = 136 + 60 = 196; AC = 14 (см).

Ответ: 14 см.