Предмет: Алгебра,
автор: amirkamesh22
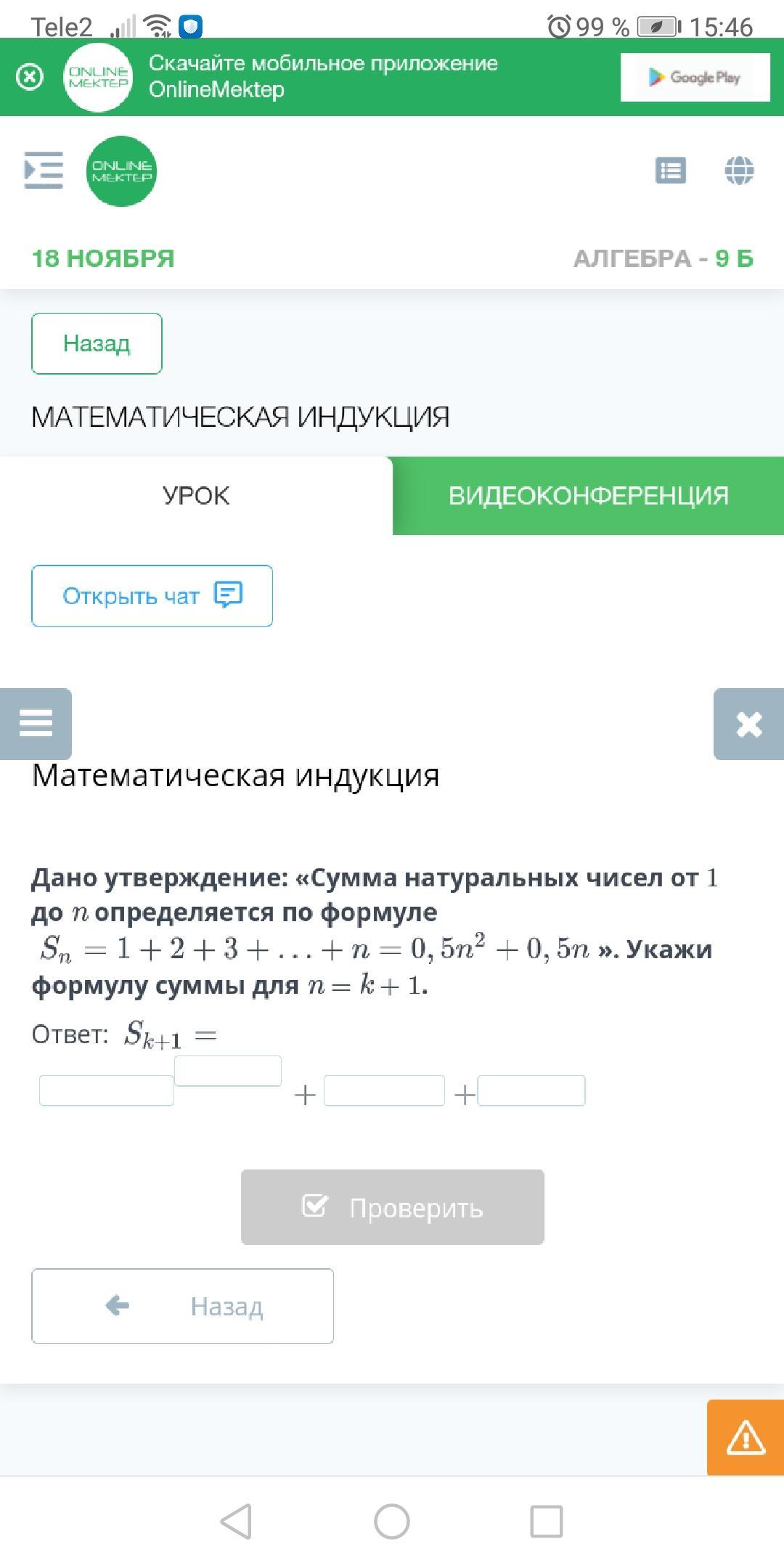
Дано утверждение: «Сумма натуральных чисел от 1 до n определяется по формуле
Sn= 1+2+3+....+n=0,5n2+0,5n>> Укажи формулу суммы для n = k + 1.
Sk+1=
Помогите пожалуста
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Дана формула суммы:
Определим формулу суммы для n = k + 1:
Похожие вопросы
Предмет: Физика,
автор: bboydevil
Предмет: Математика,
автор: nasta23671
Предмет: Литература,
автор: bezflaga
Предмет: Алгебра,
автор: lednevairina
Предмет: Геометрия,
автор: butonchik0