Предмет: Алгебра,
автор: vanopro
Решить линейное уравнение методом крамера
Приложения:
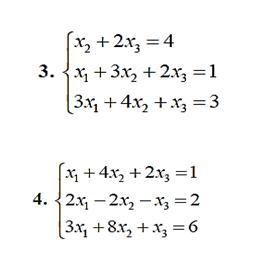
sangers1959:
Я могу решить одну систему на выбор. Баллы меня не интересуют.
если решишь оба будет просто замечательно
Тогда разбейте их на два задания по 5 баллов. Решение очень объёмное (много матриц с комментарием). Я думаю, за сегодня - справимся.
Я могу третье задание решать прямо здесь, но тогда вы потеряете баллы.
Ответы
Автор ответа:
1
Объяснение:
3.
Запишем эту систему в матричной форме: Ах=b.
Найдём определитель матрицы Δ:
Заменим 1-й столбец матрицы A на вектор столбца b:
Заменим 2-й столбец матрицы A на вектор столбца b:
Заменим 3-й столбец матрицы A на вектор столбца b:
Ответ: x₁=5, x₂=-4, x₃=4.
Здравствуйте, помогите пожалуйста https://znanija.com/task/40103541
Похожие вопросы
Предмет: Русский язык,
автор: arman87063
Предмет: Русский язык,
автор: olesyabryzgalova
Предмет: Русский язык,
автор: misssmaslova
Предмет: Математика,
автор: olyadimitriu
Предмет: Алгебра,
автор: dolli777ls