Предмет: Математика,
автор: batmadilmuratova
найти область определения функции.
Приложения:
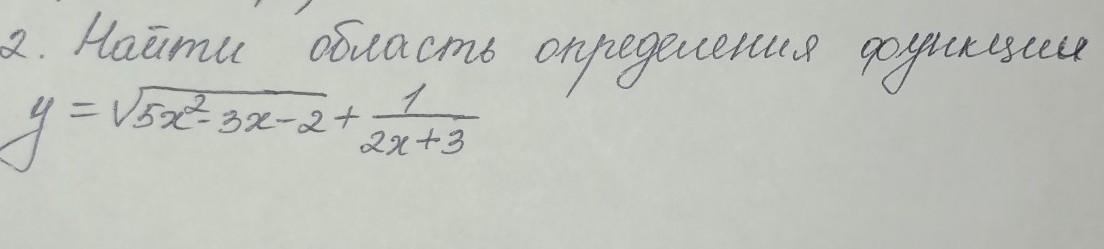
Ответы
Автор ответа:
1
Ответ:
======================================
x∈(-∞;-3/2)∪(-3/2;-2/5]∪[1;+∞)
Похожие вопросы
Предмет: Математика,
автор: karina111104
Предмет: Русский язык,
автор: pavlovi77
Предмет: Физика,
автор: Кристина24011999
Предмет: Обществознание,
автор: hikkrjrjrj4jrn
Предмет: Математика,
автор: olyadimitriu