Предмет: Алгебра,
автор: nikitakorolev2
Найти угол между прямыми
Приложения:
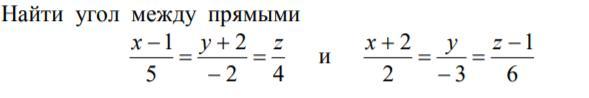
Ответы
Автор ответа:
0
Угол между прямыми есть угол между их направляющими векторами.
Направляющий вектор первой прямой = {5;-2;4}
Направляющий вектор второй прямой = {2;-3;6}
Скорее всего, С.К. прямоугольная. Поэтому
cos α = ;
cos α = ;
cos α = ;
α = arccos
nikitakorolev2:
Надеюсь верно решил
Похожие вопросы
Предмет: Математика,
автор: kamila99999
Предмет: Математика,
автор: mariyasa2015
Предмет: Русский язык,
автор: Гэтсби163
Предмет: Математика,
автор: осоатс