Question

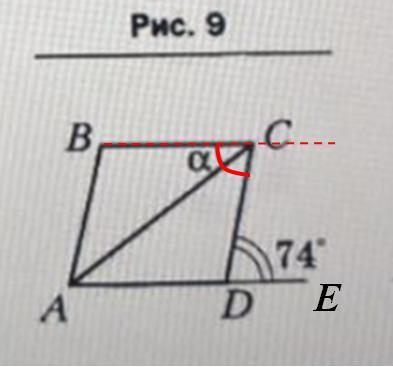
на рисунке Четырёхугольник ABCD—ромб.Найдите угол а. я

Answer 1

Ответ:

$\alpha = 37^{ \circ}$

Объяснение:

1) Раз ABCD - ромб => АВ=ВС=CD=AD ( по определению )

Раз АВ=ВС и AD=DC => ∆ABC и ∆ADC - равнобедренные => ∠BAC = ∠BCA и ∠ACD = ∠CAD

2) ∠BCA = ∠CAD как накрест лежащие при AD//BC и секущей AC

Объединяя пункты 1) и 2), получим:

∠BCA = ∠CAD = ∠ACD

Т. к. ∠CDE - внешний ∠ => ∠CAD + ∠ACD = ∠CDE

∠CDE = ∠BCA + ∠BCA

∠CDE = 2∠BCA

∠BCA = ∠CDE/2 = 74°/2 = 37°

Answer 2

Ответ:

α = 37°

Объяснение:

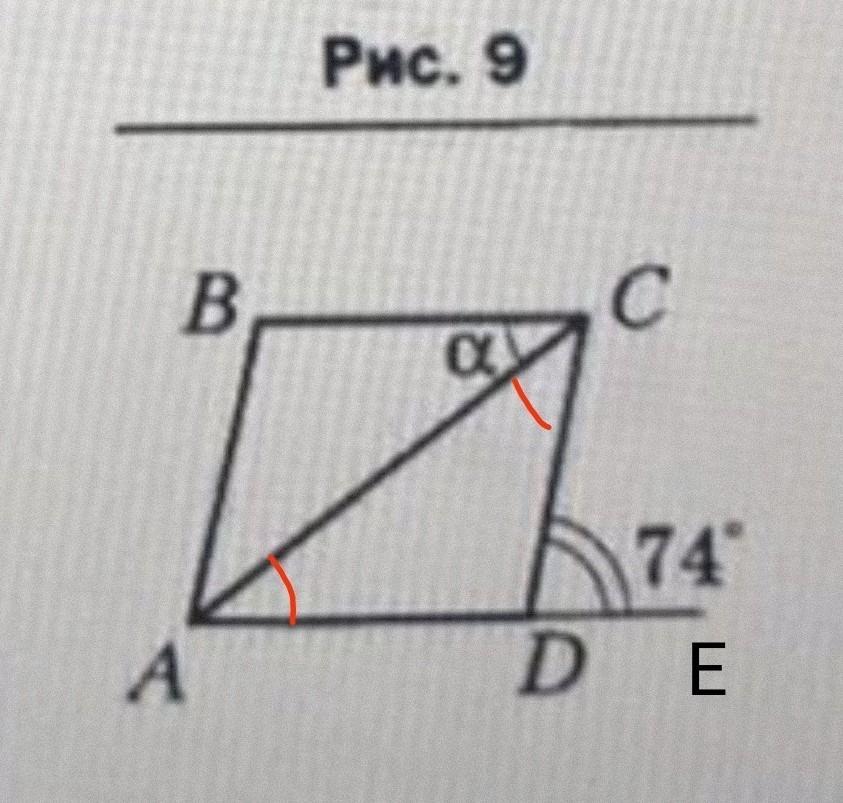
Дано (см. рисунок):

  ABCD - ромб

  ∠CDE = 74°  

Найти: α = ∠ACB.

Решение. Ромб обладает следующими нужными нам свойствами:

1) BC || AD, AB || DC;

2) Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).

Проведём прямую BC. Тогда по свойству 1 прямые BC и AD параллельны и при параллельных прямых BC и AD прямая AC будет секущей. Поэтому углы ∠CDE и ∠BCD - накрест лежащие.

Вспомним свойство накрест лежащих углов: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Отсюда: ∠BCD = ∠CDE = 74°.

По свойству 2 диагональ ромба AC делит угол ∠BCD пополам. Тогда

α = ∠ACB = ∠BCD:2 = 74°:2 = 37°.