Предмет: Алгебра,
автор: olejnikangelina479
помогите пжжжжжжжжжжж
Приложения:
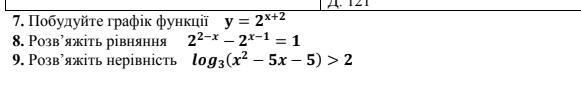
Ответы
Автор ответа:
0
Ответ:
нехай
t1 не підходить бо -4<0
повернемось до заміни
відповідь: х=1
.........
{x² - 5x - 5 > 0
{х²- 5x - 5 > 3²
тепер знайдемо переріз розв'язку цих нерівностей :
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: plisserg
Предмет: Биология,
автор: миксерка
Предмет: Русский язык,
автор: arevik20042007
Предмет: Физика,
автор: Shiro228
Предмет: Алгебра,
автор: marusya13catoyog7r