Предмет: Математика,
автор: hachapyribro
Тело проходит 5 одинаковых участков пути,
имея различные скорости: первый участок – со скоростью 1 м/с, а скорость
каждого последующего равна сумме скоростей двух предыдущих участков.
Чему равно время движения тела, если первую половину пути тело шло
60,75 с?
Ответы
Автор ответа:
3
По условию :
Скорость на участке пути до первого неизвестна, эта скорость понадобится, чтобы посчитать скорость на втором участке пути.
Пусть скорость v₀ = 0 м/с.
На первом участке: v₁ = 1 м/с.
На втором участке: v₂ = v₀ + v₁ = 0 м/с + 1 м/с = 1 м/с.
На третьем участке: v₃ = v₁ + v₂ = 1 м/с + 1 м/с = 2 м/с.
На четвёртом участке: v₄ = v₂ + v₃ = 1 м/с + 2 м/с = 3 м/с.
На пятом участке: v₅ = v₃ + v₄ = 2 м/с + 3 м/с = 5 м/с.
Из равенства участков пути находим отношение времени для каждого участка пути.
Так как участки пути одинаковые, то первая половина пути состоит из всего первого участка, всего второго участка и половины третьего участка.
Время прохождения первой половины пути:
По условию:
Время движения тела на всём пути:
Ответ: 81,9 с.
Приложения:
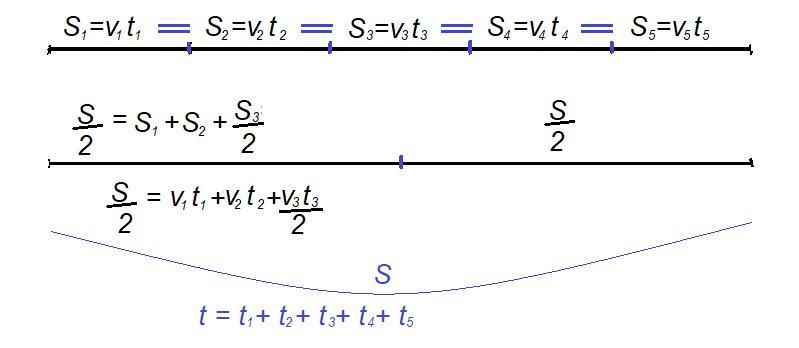
Похожие вопросы
Предмет: История,
автор: ДашаФома
Предмет: Другие предметы,
автор: nastyasap4
Предмет: Қазақ тiлi,
автор: aaa04
Предмет: Обществознание,
автор: Aleksuggg
Предмет: Математика,
автор: sonavoznaa