Предмет: Алгебра,
автор: Cocacolawolf
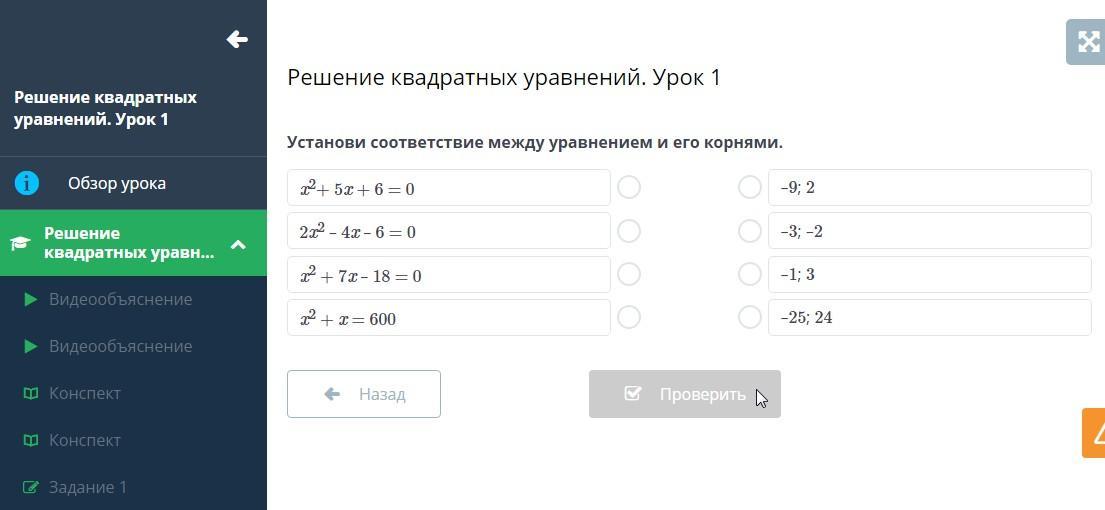
Решение квадратных уравнений. Урок 1
Установи соответствие между уравнением и его корнями.
СРОЧНО, ПОМОГИТЕ ПЛИС
Приложения:
alinasapargalieva:
????
чел ты нашел?
ДА
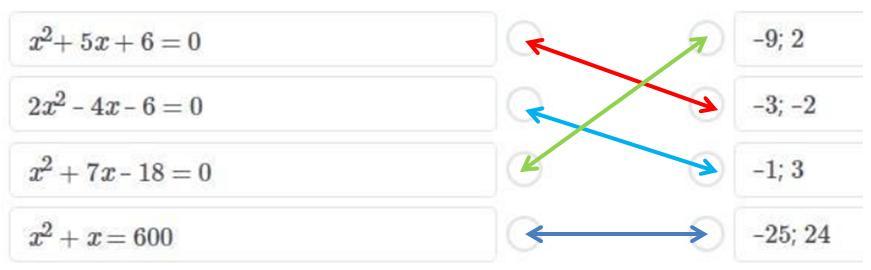
1-2, 2-3, 3-1, 4-4.
Ответы
Автор ответа:
2
Ответ и Объяснение:
Пусть дано квадратное уравнение a·x²+b·x+c=0. Если
1) D=b²-4·a·c>0, то квадратное уравнение имеет 2 корня:
2) D=b²-4·a·c=0, то квадратное уравнение имеет 1 корень:
3) D=b²-4·a·c<0, то квадратное уравнение не имеет корней!
Решение.
1) x²+5·x+6=0, a=1, b=5, c=6, D=5²-4·1·6=25-24=1=1²>0:
2) 2·x²-4·x-6=0, a=2, b= -4, c= -6, D=(-4)²-4·2·(-6)=16+48=64=8²>0:
3) x²+7·x-18=0, a=1, b=7, c= -18, D=7²-4·1·(-18)=49+72=121=11²>0:
4) x²+x=600 или x²+x-600=0, a=1, b=1, c= -600,
D=1²-4·1·(-600)=1+2400=2401=49²>0:
Установленные соответствия в приложении.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Пруцко
Предмет: Математика,
автор: vladdabroslavs
Предмет: Химия,
автор: DashaBestCat
Предмет: Математика,
автор: ЛаураКотяша