Question

помогите мне срочно сегодня надо
Задача:
Диагонали AC и BD четырехугольника ABCD равны и пересекаются в точке F. Докажите, что прямая, соединяющая середины сторон BC и AD перпендикулярна биссектрисе угла <CFD​

Answer 1

Пошаговое объяснение:

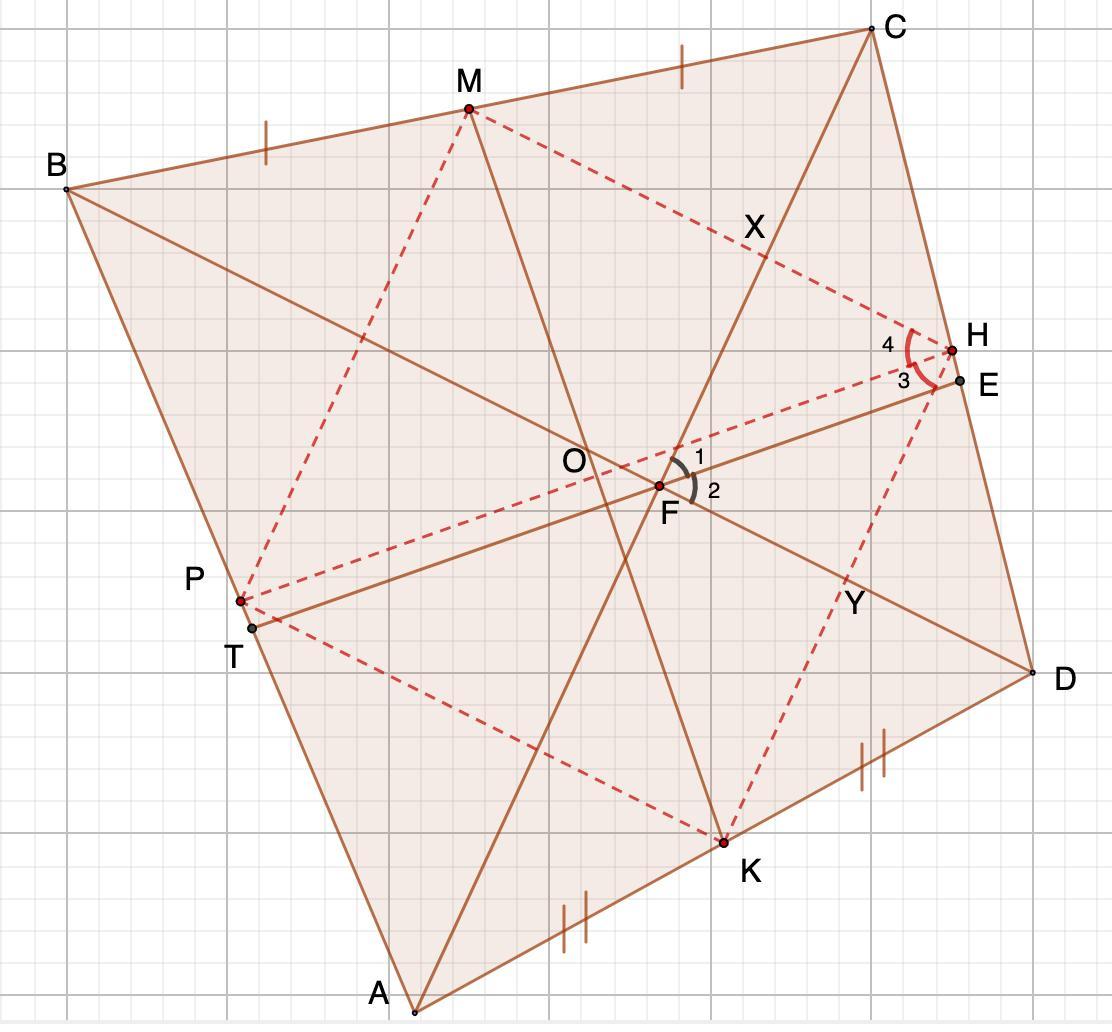
Дано: ABCD - четырехугольник;

АС=ВD - диагонали;

ВМ=МС; АК=КD;

FЕ - биссектриса ∠CFD.

Доказать: МК⊥ТЕ

Доказательство:

Дополнительное построение: Р и Н - середины АВ и СD соответственно.

Соединим точки Р, М, Н, К.

1) Рассмотрим ΔАВС.

АР=РВ (построение)

ВМ=МС (условие)

⇒РМ - средняя линия.

Средняя линия треугольника параллельна основанию и равна его половине.

$\displaystyle PM ||AC;\;\;\;PM=\frac{1}{2} AC$

2) Рассмотрим ΔАСD.

CH=HD (построение)

AK=KD (условие)

⇒KH - средняя линия.

$\displaystyle KH||AC;\;\;\;KH=\frac{1}{2}AC$

3) Рассмотрим ΔABD.

AP=PB (построение)

АК=KD (условие)

⇒ КР - средняя линия.

$\displaystyle PK||BD;\;\;\;PK=\frac{1}{2}BD$

4) Рассмотрим ΔBCD

BM=MC (условие)

CH=HD (построение)

⇒ МН - средняя линия.

$\displaystyle MH||BD;\;\;\;MH=\frac{1}{2}BD$

5) Рассмотрим РМНК.

Если две прямые параллельны третьей прямой, то они являются параллельными.

PM || AC (п.1); КН || AC (п.2) ⇒РМ || KH

PK || BD (п.3); MH || BD (п.4) ⇒ РК || MH

⇒ РМНК - параллелограмм.

$\displaystyle PM=KH=\frac{1}{2}AC\\\\PK=MH=\frac{1}{2} BD$

AC=BD (условие)

⇒ PM=KH=PK=MH ⇒PMHK - ромб.

Диагонали ромба перпендикулярны и являются биссектрисами углов ромба.

⇒ ∠3=∠4;  РН ⊥ МК.

6) Рассмотрим FXHY - параллелограмм (по определению)

∠3=∠4 (п.5)⇒ НО - биссектриса ∠ХНY

∠1=∠2 (условие), то есть FE - биссектриса ∠XFY

Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.

⇒ HO || FE

7)  HO || FE (п.6); РН ⊥ МК (п.5)

Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

⇒ ТЕ ⊥ МК