Предмет: Алгебра,
автор: myfamilytda
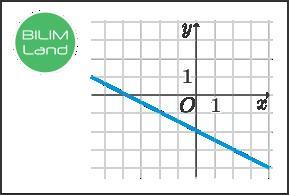
Дам 35. Укажи формулы линейных функций, графики которых проходят параллельно графику линейной функции, изображенному на рисунке.
Верных ответов: 2
y = – 0,5x – 8
y = – 4x – 3
y = – 2x + 6
y = – 4x + 8
y = – 2x – 8
y = – 0,5x + 3
Приложения:
sajdulla07:
-05х+3 -05х-8
спс
Спасибо!
Ответы
Автор ответа:
1
Ответ:
y = –0,5·x – 8 и y = –0,5·x + 3
Объяснение:
График линейной функции, изображенный на рисунке проходит через точки (-4; 0) и (0; -2). Будем искать уравнение линейной функции, то есть прямой, в виде y = k·x + b.
Подставляя в уравнение функции координаты точек получим систему уравнений и решим:
Значит, искомая функция имеет вид: y = –0,5·x – 2.
Известно, что если графики линейных функций y = k₁·x + b и y = k₂·x + b параллельны, то угловые коэффициенты равны, то есть k₁ = k₂.
В силу этого среди заданных только графики линейных функций
y = –0,5·x – 8 и y = –0,5·x + 3
параллельны графику линейной функции y = –0,5·x – 2.
Похожие вопросы