Предмет: Математика,
автор: iamlera10401
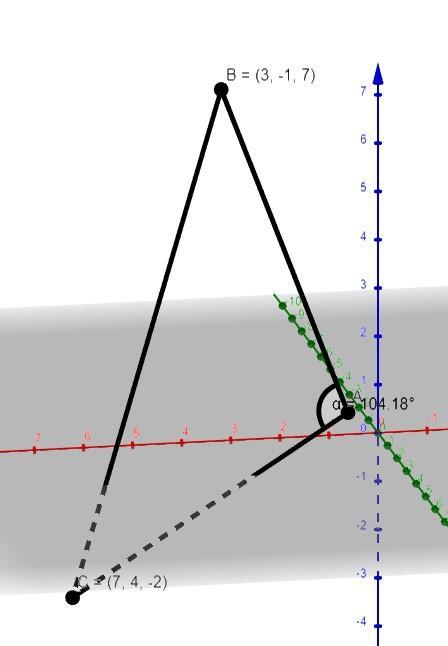
Определить внутренний угол при вершине А треугольника АВС, если А(1,2,1) В(3,-1,7) С(7,4,-2)
bezrukoff888:
Проверьте указанные координаты
Есть ощущение что есть простое решение, но координаты немного не подходят. Точно так вы их указали?
Да, все верно..
Я вернусь еще
К слову отметьте мое предыдущее решение вашего вопрос, как лучшее, если вам не сложно :)
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Составим вектора имеющие начало в точке A, а конец в B или C:
AB = {2, -3, 6}
AC = {6, 2, -3}
Скалярное произведение:
AB * AC = 12 - 6 - 18 = -12
AB*AC ≠ 0, значит вектора не перпендикулярны
Найдем длины векторов:
|AB| =
|AC| =
Пусть - искомый угол (он же угол между векторами АВ и АС)
Приравняем скалярное произведение через длины к скалярному произведению через координаты:
|AB| * |AC| * cos = -12
Выразим косинус угла
cos =
=
Выразим через обратную тригонометрическую функцию
=
Примечание:
Найти этот арккосинус можно с помощью калькулятора, окажется что наш искомый угол равен примерно 104°. Также это проверяется построением треугольника в системе координат.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: бесрлатно
Предмет: Другие предметы,
автор: epv72
Предмет: Математика,
автор: dzhuletta34
Предмет: Литература,
автор: katyakasatkina4186