Пoмoгитe рeшить cиcтeмы ypaвнeний c oднoй пeрeмeннoй

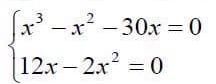
Ответы
Ответ:
В решении.
Объяснение:
Решить системы уравнений.
1) (х - 3)(2х + 1)=0
х² - 14х + 33 = 0
Решить первое уравнение:
(х - 3)(2х + 1)=0
х - 3 = 0
х₁ = 3;
2х + 1 = 0
2х = -1
х₂ = -0,5;
Решить второе уравнение:
х² - 14х + 33 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 196-132=64 √D= 8
х₁=(-b-√D)/2a
х₁=(14 - 8)/2
х₁=6/2
х₁=3;
х₂=(-b+√D)/2a
х₂=(14 + 8)/2
х₂=22/2
х₂=11
Из четырёх решений системы выбираем общие для двух уравнений:
Решение системы уравнений х=3.
2) х³ - х² - 30х = 0
12х - 2х² = 0
Решить первое уравнение:
х³ - х² - 30х = 0
х(х² - х - 30) = 0
Приравнять сомножители к нулю поочерёдно:
х₁ = 0;
х² - х - 30 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 1 + 120 = 121 √D=11
х₂=(-b-√D)/2a
х₂=(1 - 11)/2
х₂= -10/2
х₂= -5;
х₃=(-b+√D)/2a
х₃=(1 + 11)/2
х₃=12/2
х₃=6.
Решить второе уравнение:
12х - 2х² = 0
2х(6 - х) = 0
Приравнять сомножители к нулю поочерёдно:
2х = 0
х₄ = 0;
6 - х = 0
-х = -6
х₅ = 6.
Из пяти решений системы уравнений выбираем общие для двух уравнений.
Решение системы уравнений х=0, х=6.