В прямоугольном треугольнике катеты аи Б., гипотенуза - с. Найди гипотенузу прямоугольного
треугольника, если катеты равны 4 см и 6 см.
Ответ:
Ответы
Ответ:
7,2 см
Пошаговое объяснение:
По теореме Пифагора* сумма квадратов катетов равна квадрату гипотенузы:
Подставляем под АВ и ВС 4 и 6 см:
Решаем уравнение:
c ≈ 7,2
*А теперь МААААЛЕНЬКОЕ доказательство теоремки Пифагора:
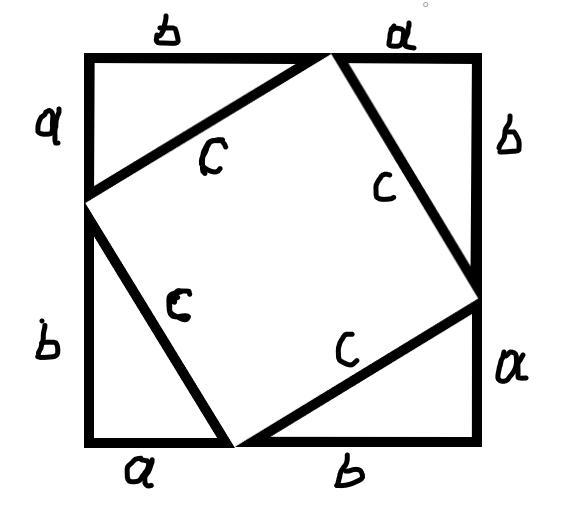
Нарисуем 4 прямоугольных треугольника с катетами А и В и с гипотенузой С как на рисунке(приложение)
Мы видим, что у нас образовался квадрат со стороной a+b. Его площадь: (a+b)^2. Внутри него квадрат со стороной с (метод построения квадрата в повороте треугольника на 90 градусов, поэтому гипотенузу мы тоже поворачивали на 90 градусов, и гипотенуза одна и та же, поэтому это можно справедливо назвать квадратом) Площадь малого квадрата: с^2. Также внутри квадрата 4 треугольника. Из них можно составить 2 прямоугольника со сторонами a и b, сумма четырех треугольников: 2ab. Поскольку мы говорим об одном и том же квадрате, можно сделать так:
Раскрываем скобки в левой части:
Вычитаем 2ab из обеих частей:
Вау! То, что нужно!