Question

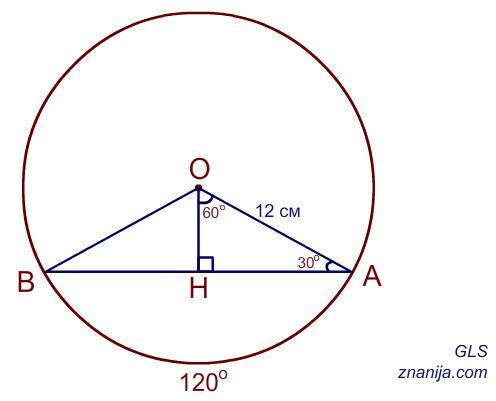
Радиус окружности равен 12 см. Хорда стягивает дугу в 120° . Определить
расстояние от центра окружности до хорды.

Answer 1

Ответ:

Расстояние от центра окружности до хорды равно 6 см.

Объяснение:

Дано: окружность с центром в т.О; радиус окружности R = 12 см; AB -хорда; дуга $\displaystyle \overset{\frown}{AB}=120^{o}$.

Найти: расстояние от центра окружности до хорды.

Решение.

Рисунок прилагается.

Проведем в окружности радиусы OB и OA.

• Угол, вершина которого лежит в центре окружности, а стороны пересекают окружность, называется центральным углом.

• Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.

Угол AOB является центральным углом. Его градусная мера равна градусной мере дуги AB.

∠AOB = 120°.

Рассмотрим ΔAOB. Он равнобедренный, так как две его стороны равны: AO = OB = R = 12 см.

Из вершины треугольника т.O опустим высоту OH на сторону AB. Высота OH является медианой и биссектрисой в равнобедренном треугольнике.

⇒ ∠AOH = ∠AOB : 2 = 120° : 2 = 60°.

В прямоугольном ΔAOH углы ∠AHO = 90°,  ∠AOH=60°;

⇒ ∠OAH = 180° - 90° - 60° = 30°.

Тогда катет OH лежит против угла 30°, его длина равна половине гипотенузы OA.

OH = OA : 2 = 12 см : 2 = 6 см.

• Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую.

Расстояние от центра окружности т.O до хорды AB равно длине высоты OH треугольника AOB  и равно 6 см.