Предмет: Геометрия,
автор: yelenavorobeva04
Найдите площадь диагонального сечения октаэдра, если его ребро равно: 1) 5 см., 2) 12 см.
Ответы
Автор ответа:
5
Ответ:1) 25 см^2; 2) 144 cv^2
Объяснение:
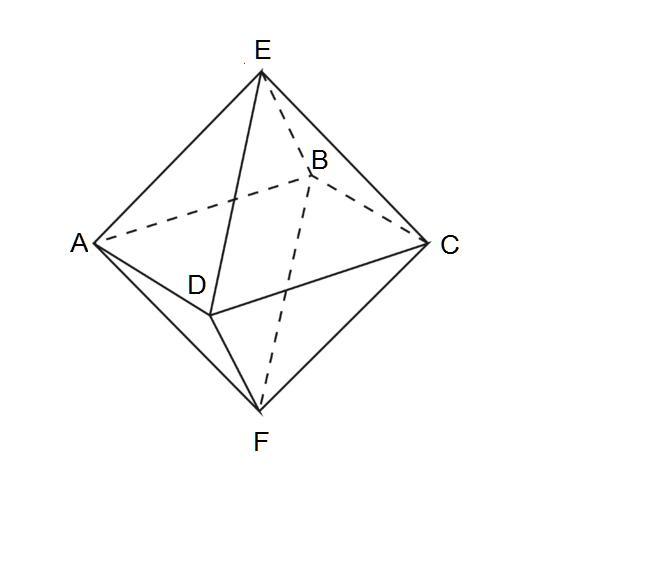
Рассмотрим основание октаэдра - квадрат ABCD. У квадрата все стороны и углы равны. Сторона квадрата - a. Диагональ квадрата делит его на два равнобедренных, прямоугольных треугольника. Диагональ равна .
Рассмотрим диагональное сечение октаэдра - ромб. Диагонали ромба равна диагонали квадрата и равна . В октаэдре диагонали ромба будут равными.
Площадь ромба находится по формуле , где d1, d2 - диагонали ромба, то есть
Тогда, 1) S=25 см^2
2) S=144 см^2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vanya715
Предмет: Математика,
автор: эльмира2004
Предмет: Химия,
автор: nadyw2013
Предмет: Литература,
автор: Bananameawlol
Предмет: Математика,
автор: predein1907