Предмет: Математика,
автор: Аноним
РЕШИТЕ ПОЖАЛУЙСТА❤️
(обчислити наближено за допомогою дифференциала)
за фигню жалоба:)
правильно пожалуйста ❤️
Приложения:
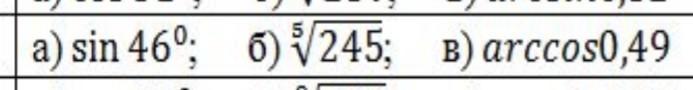
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
во всех случаях пользуемся формулой
f(x₀+ Δx) ≈ f(x₀) + f'(x₀)*Δx
теперь надо просто найти "хорошие" х₀ и Δх
в первом случае
х₀ = 45°; Δх = 1° = π/180
вот теперь вычисляем
sin 46° = sin (45° + 1°).
f'(x) = (sin x)' = cos x
sin 46° ≈ sin 45° + cos(45°) * π/180 = 1/√2 + (1/√2) * π/180 =
= (1 + π/180) / √2 ≈ (1 + 3.14/180) / 1.41 ≈ 0.7216 ≈ 0.72
во втором случае х₀ = 216; Δх = 71
f'(∛x) = 1/ 3*∛x²
f(∛216) = 6
f'(∛216) = 1/3*∛216²
дальше по формуле вычисляем
в третьем случае х₀ = 0,5; Δх = 0,01
f'(arccos x) = -1 /√(1-x²)
ну и дальше по формуле
Похожие вопросы
Предмет: Русский язык,
автор: maloli
Предмет: Русский язык,
автор: Аноним
Предмет: Информатика,
автор: Natahaaaaaaaa
Предмет: Алгебра,
автор: Tulipa
Предмет: Математика,
автор: ааааавввв