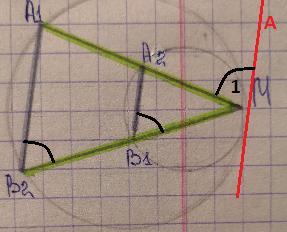
докажите, что А1В2 и А2В1 параллельны.
Ответы
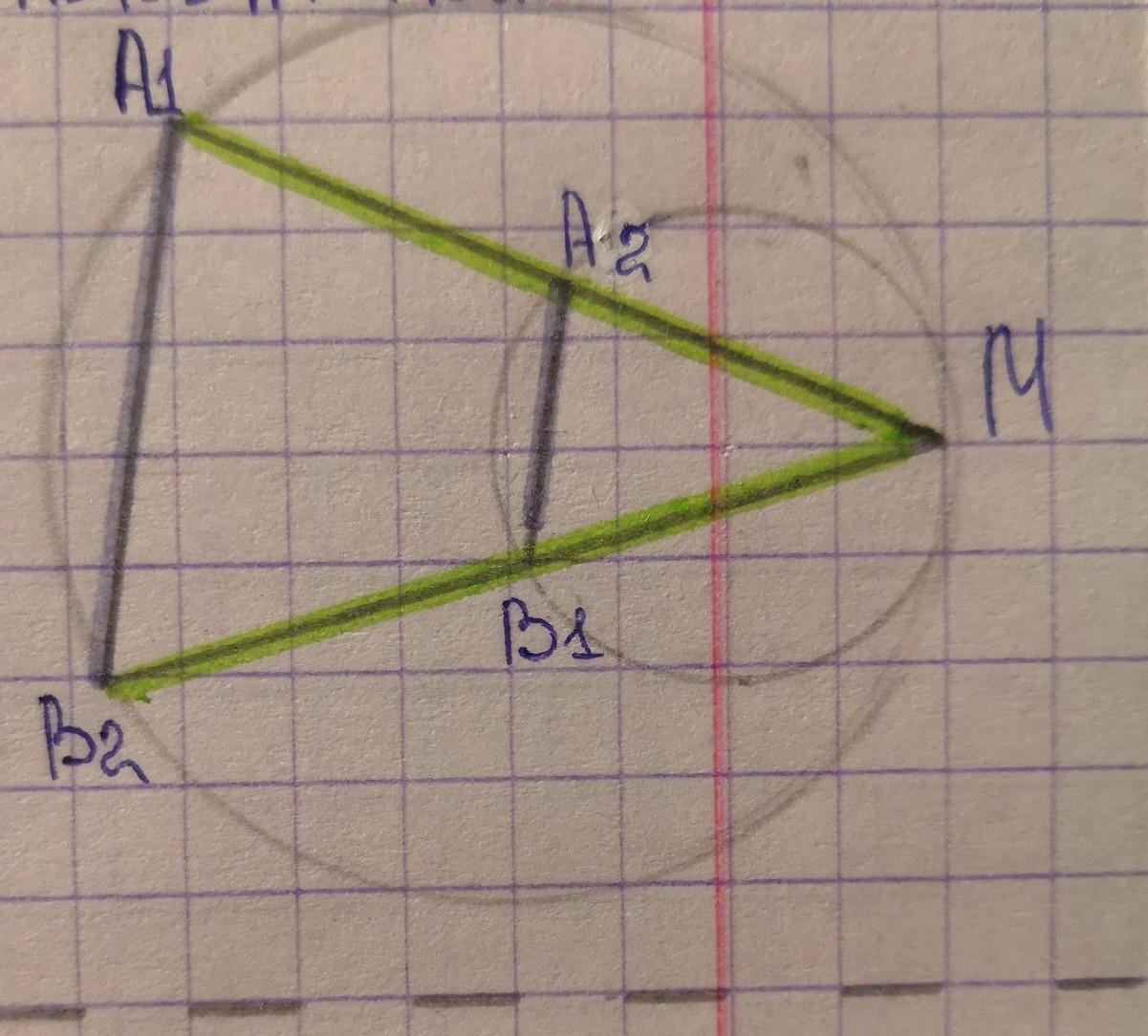
Две окружности касаются внутреннем образом в точке М. Через точку М проведены две прямые, пересекающие одну окружность в точках А₁ , В₂ , а другую в точках А₂, В₁ . Докажите А₁В₂ ║А₂В₁
Объяснение:
Проведем касательную МА . Она является касательной к обеим окружностям .
1) Для малой окружности . Угол ∠1 между касательной МА и хордой А₂М , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними : ∠1=1/2*∪А₂М
Вписанный угол ∠А₂В₁М=1/2*∪А₂М .Значит ∠1=∠А₂В₁М.
2) Для большей окружности .Угол ∠1 между касательной МА и хордой А₁М , проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними: ∠1=1/2*∪А₁М
Вписанный угол ∠А₁В₂М=1/2*∪А₁М. Значит ∠1=∠А₁В₂М .
3) Т.к. ∠1=∠А₂В₁М , ∠1=∠А₁В₂М ⇒∠А₂В₁М=∠А₁В₂М .
Тогда по признаку параллельности прямых с соответственными углами , при секущей В₂М ⇒ А₁В₂ ║А₂В₁