Question

Пропорциональные отрезки в прямоугольном треугольнике

Высота, проведенная из вершины прямого угла треугольника, равна 12 см и делит гипотенузу на части, разность которых равна 18 см. Вычисли длину гипотенузы.​

Answer 1

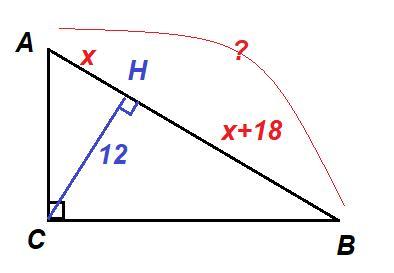
Дано:  ΔABC,   ∠ACB = 90°,   CH⊥AB,

           CH = 12 см,   BH - AH = 18 см.

Найти: AB

Решение:

BH - AH = 18 см

BH = AH + 18

В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению длин отрезков, на которые высота делит гипотенузу.

AH · BH = CH²

AH · (AH + 18) = 12²

AH² + 18AH = 144

AH² + 18AH - 144 = 0

$\dfrac D4=\left(\dfrac b2\right)^2-ac=81+144=225$

$\sqrt{\dfrac D4}=15$

AH = -9 - 15 = -24   -  не подходит по условию

AH = -9 + 15 = 6 см

AB = AH + BH = AH + AH + 18 = 6 + 6 + 18 = 30 см

Ответ: 30 см