Question

В равностороннем треугольнике ABC сторона AB =
$4 \sqrt{3}$

метра. Точка K расположена на расстоянии 3 метра от плоскости треугольника и на равном расстоянии от вершин треугольника. Определи длину отрезка BK. срочно пожалуйста ​

Answer 1

Ответ:

5 м

Объяснение:

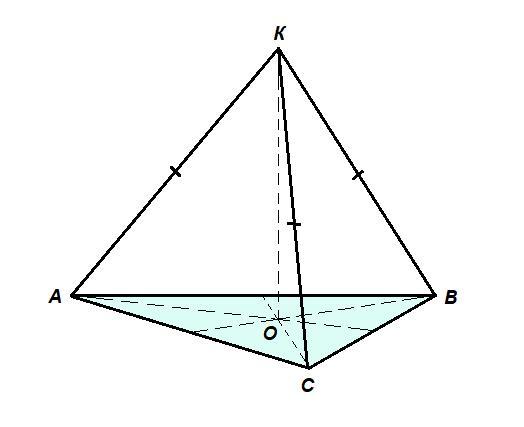
Проведем КО ⊥ (АВС).

КО = 3 м - расстояние от точки К до плоскости (АВС).

ΔКОА = ΔКОВ = ΔКОС по гипотенузе и катету:

• ∠КОА = ∠КОВ = ∠КОС = 90°
• КА = КВ = КС по условию,
• КО - общий катет.

Значит, ОА = ОВ = ОС.

Точка О равноудалена от вершин треугольника АВС, значит О - центр окружности, описанной около ΔАВС.

По формуле радиуса окружности описанной около равностороннего треугольника:

$OB=\dfrac{AB\sqrt{3}}{3}=\dfrac{4\sqrt{3}\cdot \sqrt{3}}{3}=\dfrac{4\cdot 3}{3}=4$  м

ΔКОВ:  ∠КОВ = 90°, по теореме Пифагора

 $BK=\sqrt{KO^2+OB^2}$

 $BK=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$ м