Предмет: Алгебра,
автор: isipnivlasova
Помогите решить определенный интеграл с решением, пожалуйста!
Приложения:
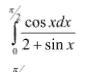
Ответы
Автор ответа:
0
Ответ:
㏑3-㏑2=㏑1.5
Объяснение:
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: agafonof63
Предмет: Математика,
автор: тосик80
Предмет: География,
автор: 17042009
Предмет: История,
автор: NoSkinArmy