Предмет: Алгебра,
автор: nikneym2000
Помогите пожалуйста
ЕСЛИ БУДЕТ ВСЕ ПРАВИЛЬНО ОТМЕЧУ, КАК ЛУЧШИЙ ОТВЕТ (НУЖНО РЕШИТЬ ДЛЯ ПРОВЕРКИ)
Приложения:
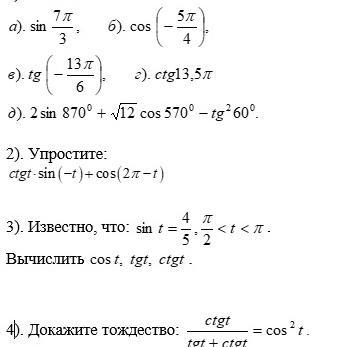
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Алгебра,
автор: Элька091
Предмет: Другие предметы,
автор: дима121505
Предмет: Математика,
автор: lelikolay5
Предмет: Информатика,
автор: fdicifigkicjrj
Предмет: Алгебра,
автор: sasha1885