Предмет: Геометрия,
автор: aleksoref
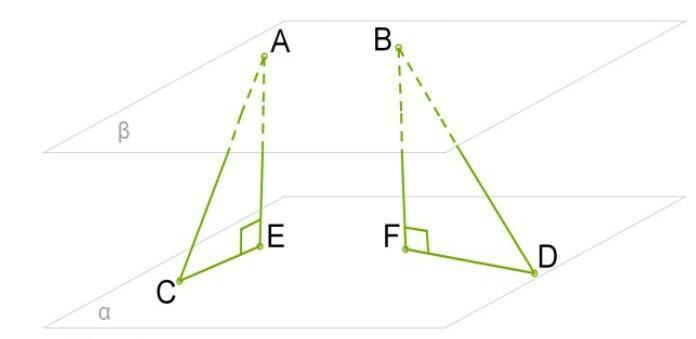
Даны параллельные плоскости α и β. Точки A и B находятся в плоскости β, а точки C и D — в плоскости α. Длина отрезка AC= 9, длина отрезка BD= 11.
Сумма проекций этих отрезков на плоскости α равна 10.
Высчитай длину проекций обоих отрезков.
1. Чтобы определить проекции отрезков AC и BD, из точек A и B надо провести
AE и BF к плоскости α.
2. AE и BF
.
3. AE и BF
как отрезки параллельных прямых между параллельными плоскостями.
4. Длины проекций CE и FD высчитаем из треугольников ACE и BDF.
Длина CE=
.
5. Длина FD=
Приложения:
Ответы
Автор ответа:
2
Ответ:
см
см
Объяснение:
Дано: A,B ∈ β; C,D ∈ α;AC = 9, BD = 11, CE + FD = 10, AE ⊥ α,β; BF = ⊥ α,β
Найти: CE,FD - ?
Решение: Так как AE ⊥ α,β; BF = ⊥ α,β по условию, тогда так как AE,BF - кратчайшее расстояние между плоскостями α и β, следовательно
AE = BF. Так как AE ⊥ α,β; BF = ⊥ α,β, то треугольник ΔAEC и ΔBFD - прямоугольные. По теореме Пифагора для треугольников ΔAEC и ΔBFD и условию составим систему уравнений:
Составим новую систему уравнений:
см.
см.
Похожие вопросы
Предмет: Русский язык,
автор: albinakuramsakova
Предмет: Английский язык,
автор: aruzhan180399
Предмет: Математика,
автор: vladpakhilkozm
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: styopka