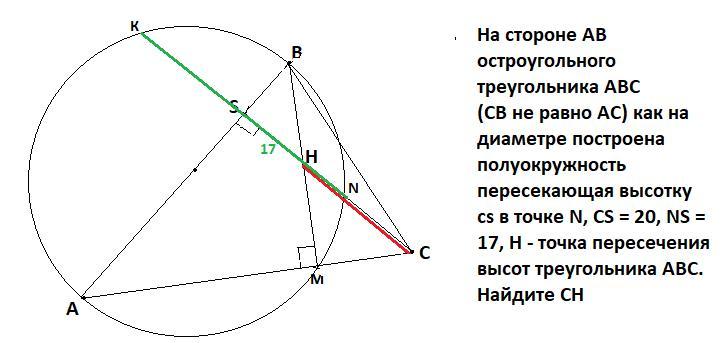
На стороне AB остроугольного треугольника ABC(CB не равно AC) как на диаметре построена полуокружность пересекающая высотку cs в точке N, CS = 20, NS = 17, H - точка пересечения высот треугольника ABC. Найдите CH
Ответы
На стороне AB остроугольного треугольника ABC(CB не равно AC) как на диаметре построена полуокружность пересекающая высотку cs в точке N, CS = 20, NS = 17, H - точка пересечения высот треугольника ABC. Найдите CH
Объяснение:
1.) Тк Н- точка пересечения высот CS и ВН Δ ABC, то точка М лежит на окружности, для которой АВ –диаметр , т.к ∠ВМА=90°.
2.) ΔSАС ∼ ΔMHC по двум углам ( общему ∠С, ∠НМС=∠АSC=90°), поэтому сходственные стороны пропорциональны
или АС*МС=СН*SC .
3.) Достроим SN ( часть перпендикуляра СS) до пересечения с окружностью . Хорда КN ⊥AB, значит КS=SN=17. Поэтому
КС= SC +KS =20+17=37 , NC= SC-SN=20-17=3 . По теореме о секущих , проведенных из точки С : NC*KC=MC*AC , 3*37=MC*AC .
4.) АС*МС=СН*SC , 3*37=СН*20 , СН=5,55