Предмет: Алгебра,
автор: cherkesovdmitry
Алгебра 10 класс, тригонометрия. Помогите
Приложения:
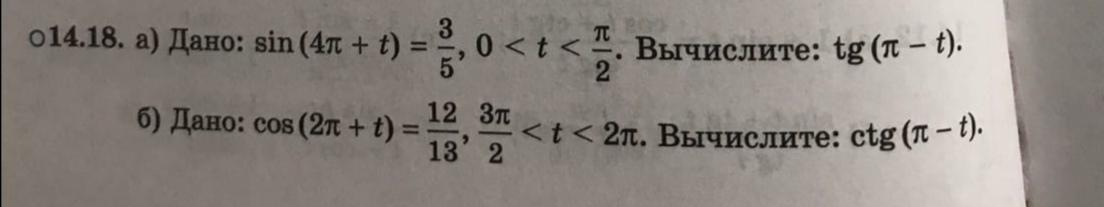
Ответы
Автор ответа:
0
14.18
а)
Так как t - угол находится в первой четверти, значит:
б)
Так как t - угол находится в четвертой четверти, значит:
Похожие вопросы
Предмет: Русский язык,
автор: vera110307
Предмет: Английский язык,
автор: Katiusa431
Предмет: Математика,
автор: Nikita18052004
Предмет: Алгебра,
автор: kcuxa03082004
Предмет: Физика,
автор: Albina1902