Question

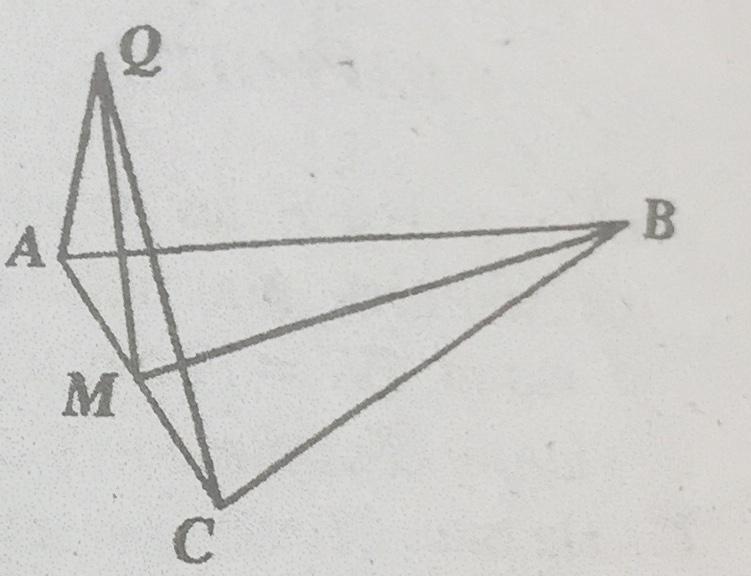
На рис. 19 изображено равнобедренный треугольник ABC (AB = BC), M - середина стороны AC. Через точку M проведена прямая MQ, перпендикулярной прямой BM. Докажите, что прямая BM перпендикулярна к плоскости AQC.

Answer 1

Ответ:

решение смотри на фотографии

Объяснение:

Answer 2

М- середина АС, значит, ВМ- медиана ΔАВС, но она проведена к основанию АС равнобедренного треугольника АВС, значит, является и высотой, т.е.  ВМ⊥АС, по условию МQ⊥ВМ.

Значит, прямая ВМ перпендикулярна двум пересекающимся прямым плоскости АQC, конкретнее,  MQ и AС,

и по признаку перпендикулярности прямой и плоскости, т.е.

если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

ВЫВОД.  ВМ⊥ (АQC), доказано.