Предмет: Геометрия,
автор: ksayrend
ДАЮ 70 БАЛЛОВ
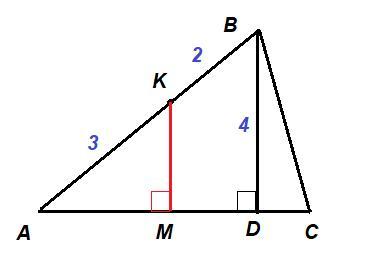
На стороне AB остроугольного треугольника ABC отмечена точка K. Найдите расстояние от точки K до стороны AC, если AK=3, BK=2, а высота BD равна 4
Ответы
Автор ответа:
10
Дано: ΔABC - остроугольный;
K∈AB; AK = 3; BK = 2;
BD⊥AC; BD = 4
Найти: d (K; AC)
Решение:
Опустим из точки К перпендикуляр к стороне АС:
KM⊥AC
Расстоянием от точки К до стороны АС будет длина перпендикуляра КМ.
ΔAMK и ΔADB прямоугольные.
ΔAMK ~ ΔADB по общему острому углу А.
Ответ: расстояние от точки К до стороны АС равно 2,4.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bokbok01
Предмет: Физика,
автор: keksik077
Предмет: Українська мова,
автор: SofkA12
Предмет: Геометрия,
автор: Абдуаханова006
Предмет: Информатика,
автор: DashaOlh