Предмет: Математика,
автор: elenasergeeva675
Помогите с неопределенным интегралом,срочно
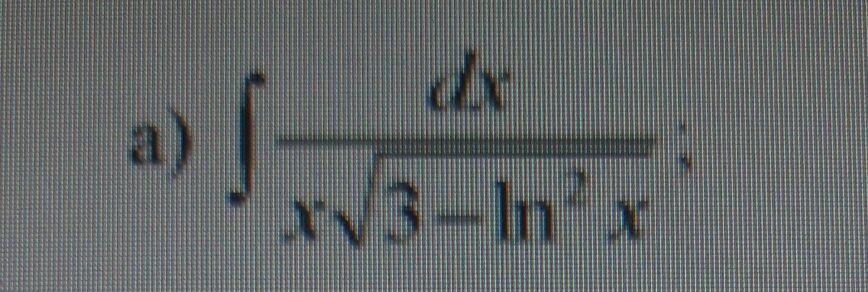
1) ∫ dx (числитель)/ x√3-In^2x(знаменатель)
2) ∫ e^2x cos (e ^2x-1)dx
Приложения:
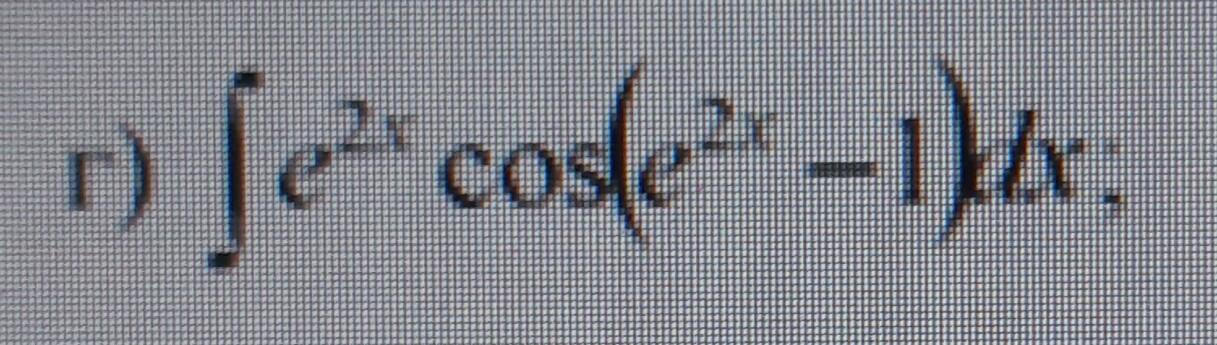
elenasergeeva675:
Если бы было понятно,я бы не спрашивала,распишите,пожалуйста,в ответе,и баллы дадут
теперь с фото
2х
Ответы
Автор ответа:
1
Ответ:
смотри ниже
Пошаговое объяснение:
Оба задания на замену дифференциала.
1) dx/x=dlnx, получаем , замена переменной y=lnx
, а это табличный интеграл.
возвращаемся к переменной x и получаем ответ:
2)Загоняем экспоненту под дифференциал:
под интегралом не хватает двойки (2), поэтому умножим подынтегральное выражение на (2/2) и получим:
теперь замена переменной:
вроде так как-то.
З.Ы. нули в пределах интеграла отсутствуют, тут просто редактор формул без пределов интеграл не рисует.
спасибо огромное
Похожие вопросы
Предмет: Русский язык,
автор: MsDaria2017
Предмет: Обществознание,
автор: skolotenok1
Предмет: Математика,
автор: varvarasokl
Предмет: Информатика,
автор: гульбарчын19
Предмет: Алгебра,
автор: мегамозг114