Предмет: Алгебра,
автор: 6YarikVodila9
Найдите предел, пожалуйста, легко решается, просто я не очень умный)
Приложения:
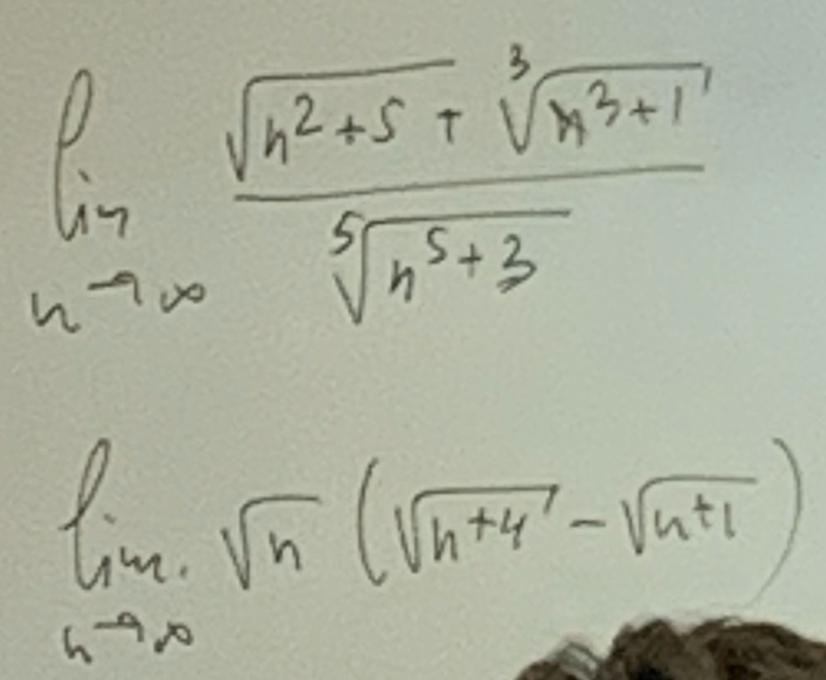
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: achalikyan
Предмет: Химия,
автор: liyul45
Предмет: Математика,
автор: nik10983