Здравствуйте. Помогите пожалуйста по геометрии. Даю 100 баллов. 10 класс. Тема: Перпендикуляр и наклонная. Теорема о троих перпендикуляров.
1. С точки M до плоскости альфа проведены наклонную MN. Найдите длину наклонной, если длина ее проекции на плоскость альфа равна 8 см, а точка M удалена от плоскости альфа на 6 см.
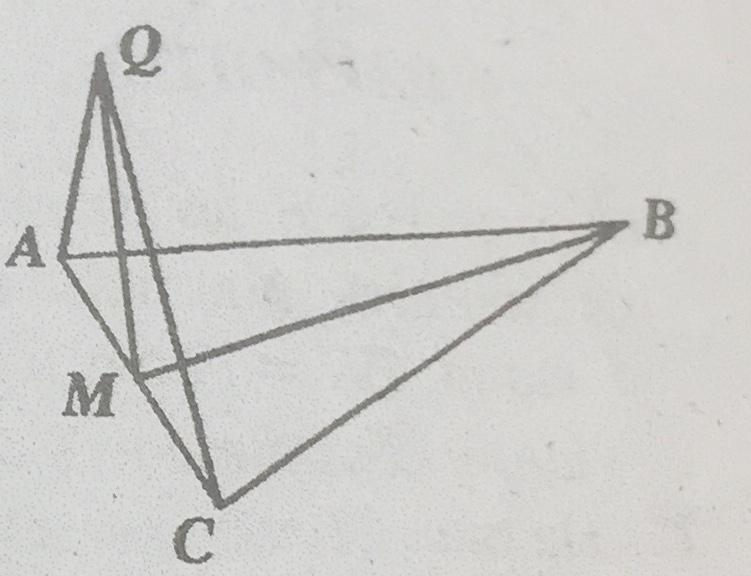
2. На рис. 19 изображено равнобедренный треугольник ABC (AB = BC), M - середина стороны AC. Через точку M проведена прямая MQ, перпендикулярной прямой BM. Докажите, что прямая BM перпендикулярна к плоскости AQC.
Ответы
1.
Только что решал эту же задачу. /прошу прощения, без чертежа, нет такой возможности, но прямоугольный треугольник, надеюсь, начертить легко./ Узловые моменты объясняю.
Она на применение теоремы Пифагора. Здесь наклонная MN- гипотенуза, проекция наклонной на плоскость α, равная 8см, это катет. А расстояние до плоскости, подлежащее определению, это другой катет прямоугольного треугольника. Треугольник египетский. Два катета 6см и 8 см, значит, гипотенуза 10 см
Ответ 10 см
2.
М- середина АС, значит, ВМ- медиана ΔАВС, но она проведена к основанию АС равнобедренного треугольника АВС, значит, является и высотой, т.е. ВМ⊥АС, по условию МQ⊥ВМ.
Значит, прямая ВМ перпендикулярна двум пересекающимся прямым плоскости АQC, конкретнее, MQ и AС,
и по признаку перпендикулярности прямой и плоскости, т.е.
если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
ВЫВОД. ВМ⊥ (АQC), доказано.