Question

Здравствуйте. Помогите пожалуйста по геометрии. Даю 100 баллов. 10 класс. Тема: Перпендикуляр и наклонная.
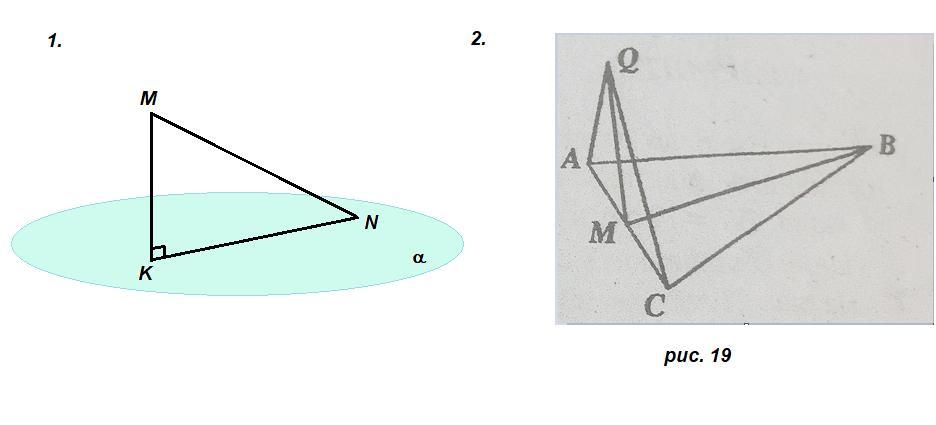
1. С точки M до плоскости альфа проведены наклонную MN. Найдите длину наклонной, если длина ее проекции на плоскость альфа равна 8 см, а точка M удалена от плоскости альфа на 6 см.
2. На рис. 19 изображено равнобедренный треугольник ABC (AB = BC), M - середина стороны AC. Через точку M проведена прямая MQ, перпендикулярной прямой BM. Докажите, что прямая BM перпендикулярна к плоскости AQC.

Answer 1

Ответ:

1. 10 см

Объяснение:

1.

Расстояние от точки до плоскости равно длине перпендикуляра, проведенного из точки к плоскости.

Проведем МК - перпендикуляр к плоскости α.

МК = 6 см - расстояние от точки М до плоскости.

KN = 8 см - проекция наклонной MN на плоскость.

Из прямоугольного треугольника MNK по теореме Пифагора:

MN = √(MK² + NK²) = √(6² + 8²) = √(36 + 64) = √100 = 10 см

2.

Признак перпендикулярности прямой и плоскости:

• если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна плоскости.

ВМ⊥MQ по условию,

ВМ⊥АС, так как медиана равнобедренного треугольника, проведенная к основанию, является высотой,

MQ∩AC = M, значит

ВМ ⊥ (AQC) по признаку.