Предмет: Алгебра,
автор: tsukishima666
Помогите пожалуйста !!!!
Приложения:
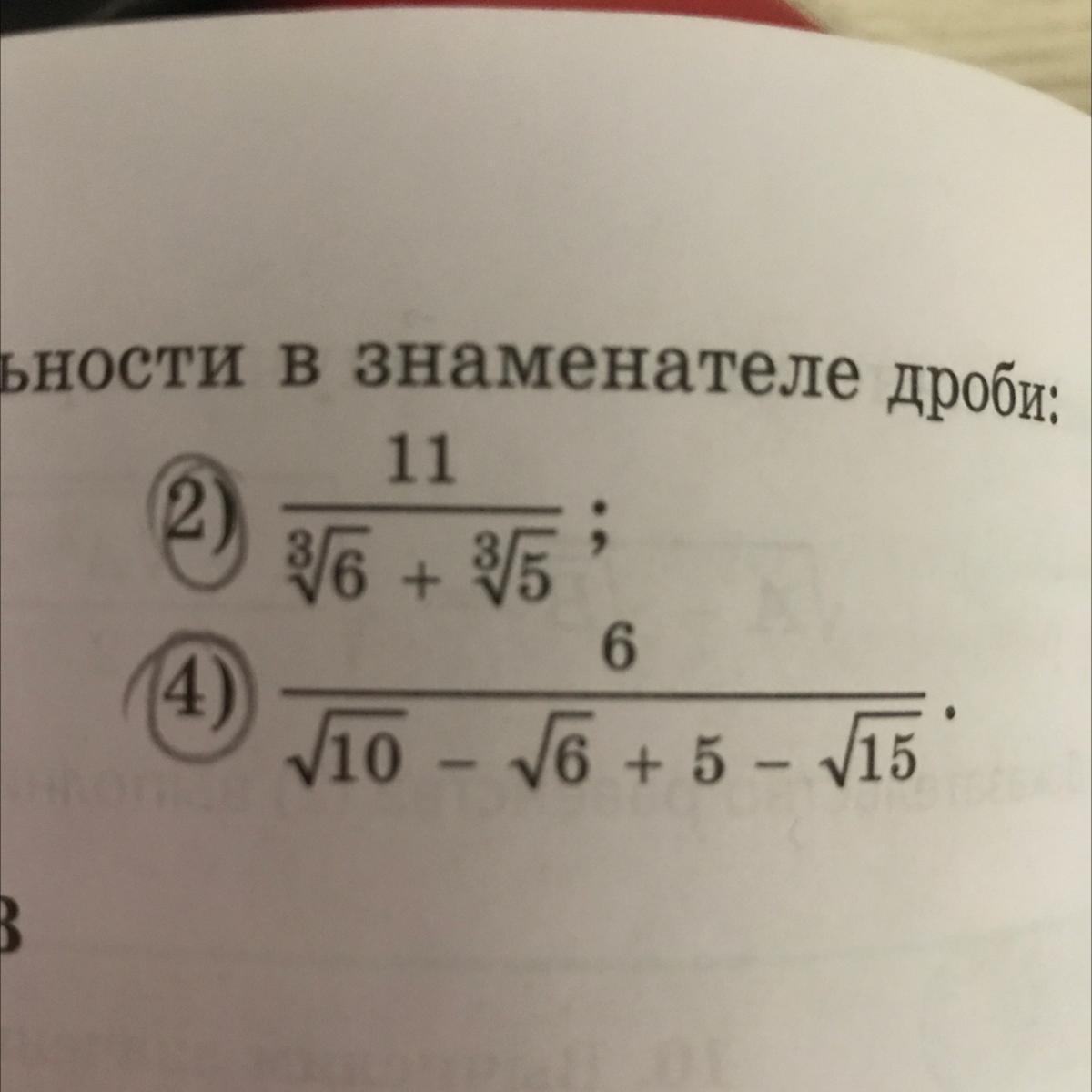
Ответы
Автор ответа:
0
Ответ:
Объяснение:
tsukishima666:
Спасибо а можно 4 как то сфоткать а то я только половину решения вижу
Похожие вопросы
Предмет: Українська мова,
автор: liza098056
Предмет: Алгебра,
автор: duska99
Предмет: Математика,
автор: vanish20044
Предмет: Литература,
автор: ancetro
Предмет: История,
автор: mashapantykina4