Question

СРОЧНО!!! Расположите числа, начиная с правого неизвестного по часовой стрелке.
2,17/27,10/9,1/6, 1 1/2,2 4/7.

Answer 1

Ответ:

$2\frac{4}{7}; 2; 1\frac{1}{2};\frac{17}{27}; \frac{1}{6}; \frac{10}{9}.$

Пошаговое объяснение:

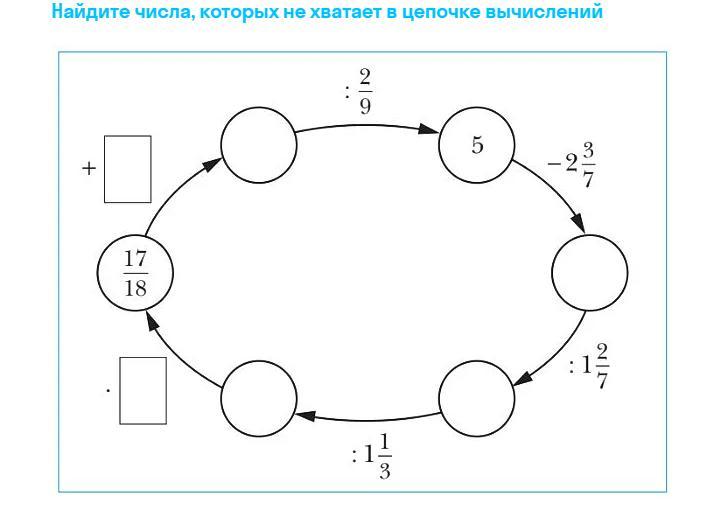
У нас известна "точка отправления" в этой цепочке, это число $5$.

Далее, согласно стрелочке, идущей вправо, из числа 5 вычитается дробь $2\frac{3}{7}$. Для этого представим данную дробь в виде неправильной, для этого в числителе основание знаменателя умножаем на целую часть дроби, и прибавляем "остаток" из числителя, оставляя нетронутым сам знаменатель: $2\frac{3}{7}=\frac{7*2+3}{7}=\frac{17}{7}$.

Число $5$ также для удобства необходимо представить в виде дроби со знаменателем $7$: $\frac{35}{7}$.

Теперь мы имеем право без проблем вычесть одну дробь из другой:

$\frac{35}{7}-\frac{17}{7}=\frac{18}{7}=2\frac{4}{7}$.

Далее, согласно стрелочке у нас идет деление полученной дроби на дробь $1\frac{2}{7}$, которую мы тоже переводим в неправильную и получаем: $1\frac{2}{7}=\frac{7*1+2}{7}=\frac{9}{7}$.

Теперь чтобы поделить одну дробь на другую, необходимо вторую дробь перевернуть наверх знаменателем и произвести умножение этих дробей: $\frac{18}{7}:\frac{9}{7}=\frac{18}{7}*\frac{7}{9}=\frac{2*1}{1*1}=2$.

Далее идет еще одно деление на дробь $1\frac{1}{3}$. Переводим дробь в неправильную: $1\frac{1}{3}=\frac{1*3+1}{3}=\frac{4}{3}$.

Теперь число переводим в дробь со знаменателем $3$:

$2=\frac{6}{3}$

А сейчас поделим $\frac{6}{3}$ на $\frac{4}{3}$:

$\frac{6}{3}:\frac{4}{3}=\frac{6}{3}*\frac{3}{4}=\frac{3*1}{1*2}=\frac{3}{2}=1\frac{1}{2}$.

Теперь нам необходимо найти число, на которое необходимо умножить полученную дробь, чтобы получить $\frac{17}{18}$.

Можем составить уравнение:

$\frac{3}{2}*x=\frac{17}{18}$

Отсюда неизвестное число в левом нижнем прямоугольнике будет равно:

$x=\frac{17}{18}:\frac{3}{2}\\\\x=\frac{17}{18}*\frac{2}{3}\\\\x=\frac{17*2}{18*3}=\frac{17*1}{9*3}=\frac{17}{27}$.

Нам осталось найти два числа в этой цепочке. Пойдем от обратного, из числа $5$ направо.

Неизвестное число делится на дробь $\frac{2}{9}$ и получается число $5$. Поэтому прибегнем к составлению уравнения:

$x:\frac{2}{9}=5\\\\\frac{x}{1}*\frac{9}{2}=5\\\\\frac{9*x}{2}=5\\\\9*x=5*2\\\\9*x=10\\\\x=\frac{10}{9}$

Теперь нам необходимо найти оставшееся последнее число в левом верхнем прямоугольнике. Нам известно итоговое число и исходное, поэтому чтобы найти промежуточное число, необходимо из итогового вычесть начальное:

$\frac{10}{9}-\frac{17}{18}$

Нужно привести дроби к общему знаменателю, для этого первую дробь домножим на 2:

$\frac{10}{9}-\frac{17}{18}=\frac{10*2}{9*2}-\frac{17}{18}=\frac{20}{18}-\frac{17}{18}=\frac{3}{18}=\frac{1}{6}$.

Итого, слева направо по часовой стрелке, начиная с числа $5$, получим цепочку чисел вместо пропусков:

$2\frac{4}{7}; 2; 1\frac{1}{2};\frac{17}{27}; \frac{1}{6}; \frac{10}{9}.$