Question

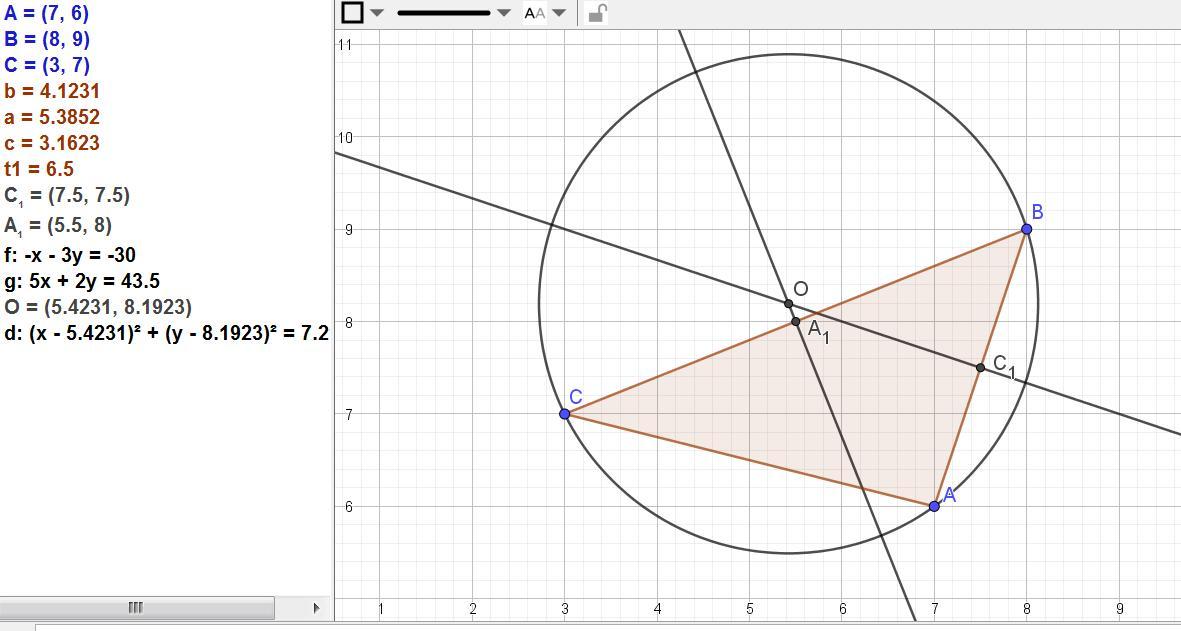
Даны точки А(7; 6), B(8; 9) и C(3; 7)
Записать уравнение описанной окружности треугольника ABC

Answer 1

Даны точки А(7; 6), B(8; 9) и C(3; 7).

Для уравнения окружности нужны координаты её центра и радиус.

Найдём уравнения двух срединных перпендикуляров и точка их пересечения и есть центр описанной окружности.

Вектор АВ = (1; 3), уравнение АВ: (x - 7)/1 = (y - 6)/3 или в общем виде

3x - y - 15 = 0.

Вектор ВC = (-5; -2), уравнение BC: (x - 8)/(-5) = (y - 9)/(-2) или в общем виде 2x - 5y + 29 = 0.

Находим координаты середин сторон АВ и ВС.

С1 = (А+В)/2 = (7,5; 7,5), А1 = (В+С)/2 = (5,5; 8)

Уравнения перпендикуляров через точки (координаты Аи В меняем на -В и А):

С1: x + 3y + C = 0,  подставим координаты точки С1:

1*7,5 + 3*7,5 + С = 0, отсюда С = -30, уравнение x + 3y - 30 = 0

A1: 5x + 2y + C = 0, подставим координаты точки А1:

5*5,5 + 2*8 + С = 0, отсюда С = -43,5.

Уравнение 5x + 2y - 43,5 = 0 или с целыми коэффициентами

10x + 4y - 87 = 0.

Находим центр окружности, решая систему:

{x + 3y - 30 = 0,

{10x + 4y - 87 = 0.

Получаем х(О) = 141/26 ≈ 5,42308, у(О) = 639/78 ≈ 8,19231.

Радиус равен 2,700536874  (находим по двум точкам А и О).

Ответ: уравнение описанной окружности

(x - (141/26))² + (y - (639/78))² = 2,700536874².