Question

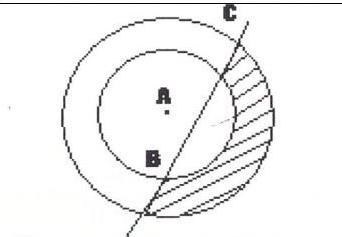
Задана точка A(0,0) — центр двух концентрических окружностей, которые пересекаются прямой в точках В(-1,-1), С(4,2)
Найти закрашенную область

Answer 1

В задании, очевидно, надо определить ПЛОЩАДЬ закрашенной фигуры.

Она представляет собой разность сегментов двух заданных кругов.

Радиусы их равны:

АВ = √((-1)² + (-1)²) = √2,

АС = √(4² + 2²) = √20.

Площадь сегмента круга находится, как разность площади сектора AOB и площади равнобедренного треугольника AOB, выраженную через угол.

Sсегм =  (R² /2)(πα° /180°  −sin(α°)).

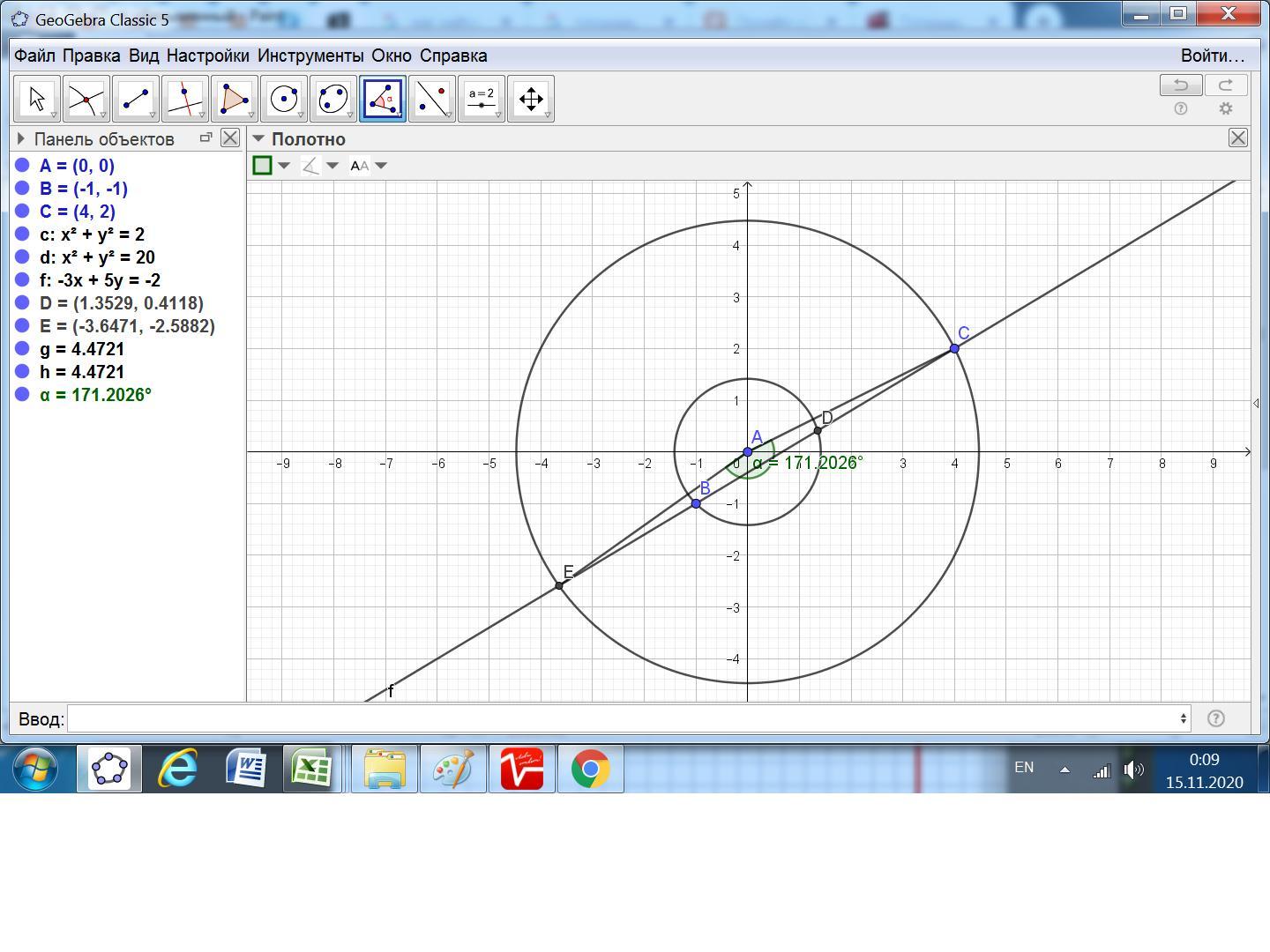
Находим координаты точек пересечения окружностей с заданной прямой решением систем из уравнения окружности и прямой.

Точка Е: x² + y² = 20,  3x - 5y - 2 = 0. E(-62/17; -44/17).

Точка D: x² + y² = 2,  3x - 5y - 2 = 0. D(23/17; 7/17).

Площади сегментов равны:

Площадь         Площадь

28.3511                  2.1810

Ответ: S = 28.3511 - 2.1810  = 26,1701 .