Предмет: Математика,
автор: 3ton228
Помогите пожалуйста, СРОЧНО!!!
Найти общее решение дифференциального уравнения. РАСПИСАТЬ РЕШЕНИЕ
Приложения:
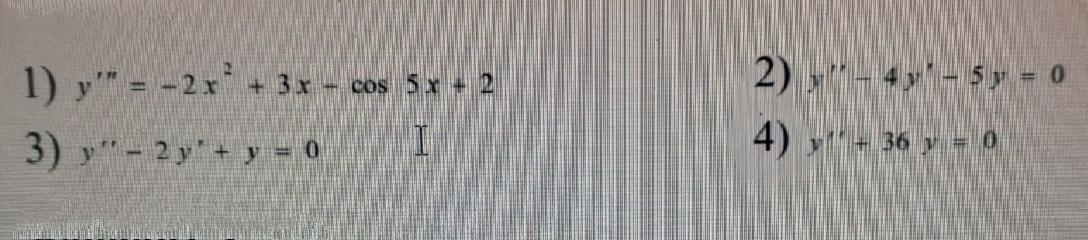
3ton228:
Помогите
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: Варвара1012
Предмет: Английский язык,
автор: popovasvet28
Предмет: Алгебра,
автор: VANO1291
Предмет: Математика,
автор: каз14