Предмет: Математика,
автор: Аноним
Решите логарифмические неравенства
Приложения:
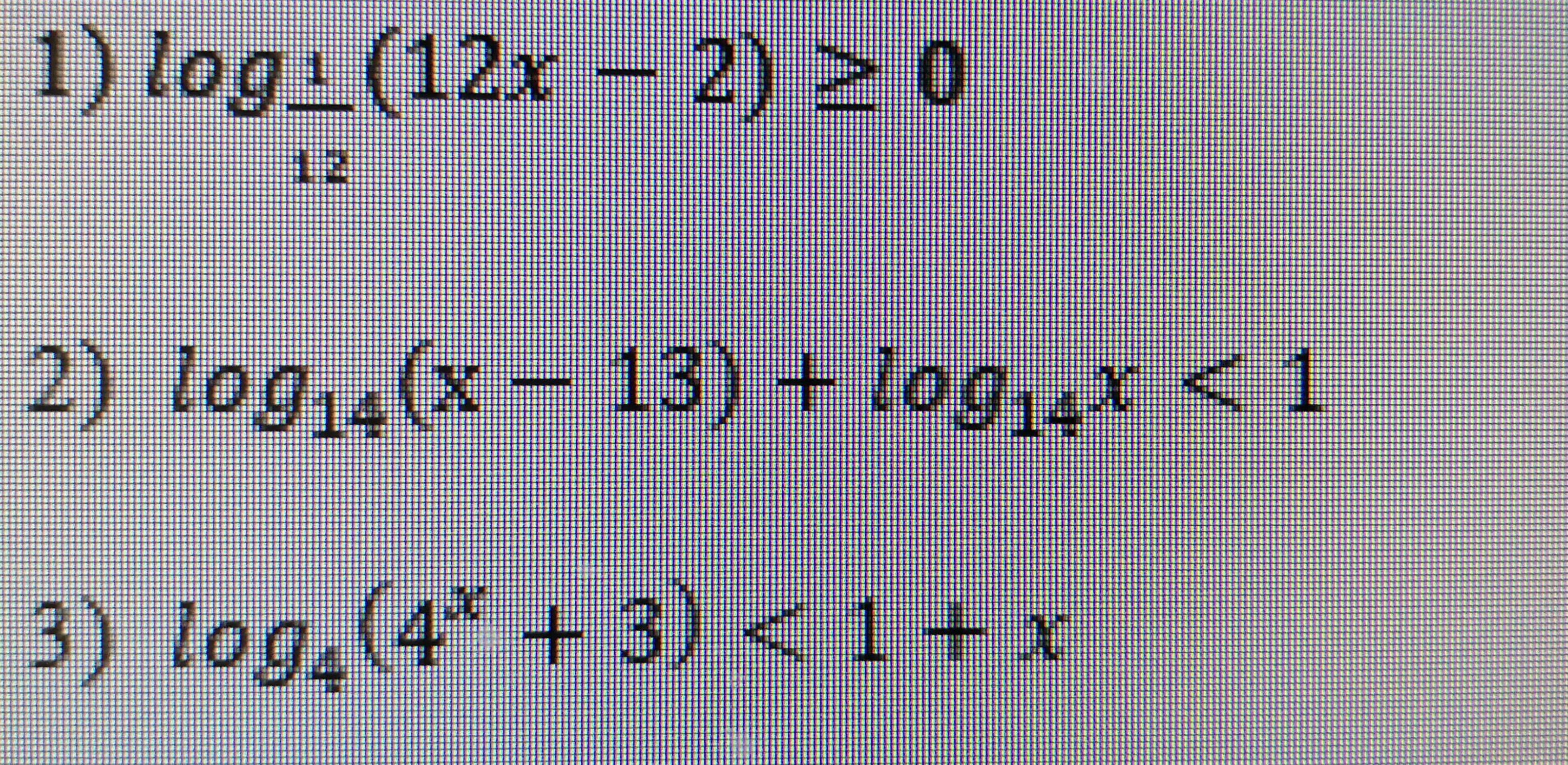
Ответы
Автор ответа:
1
1)
2)
3)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: adorokhuna
Предмет: Русский язык,
автор: sherstunov04
Предмет: Геометрия,
автор: Аноним
Предмет: Музыка,
автор: 50Anna50