Question

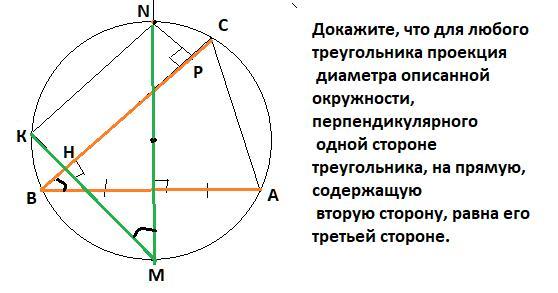
Докажите, что для любого треугольника проекция
диаметра описанной окружности, перпендикулярного
одной стороне треугольника, на прямую, содержащую
вторую сторону, равна его третьей стороне.

Answer 1

Решение : ///////////////////////////////////////////////////

Answer 2

Докажите, что для любого треугольника проекция  диаметра описанной окружности, перпендикулярного  одной стороне треугольника, на прямую, содержащую  вторую сторону, равна его третьей стороне.

Объяснение:

Пуcть из концов диаметра опущены перпендикуляры NP и MH на сторону ВС .Пусть МН пересекает окружность в т К.

Четырехугольник РNKH - прямоугольник : ∠Р=∠Н=90° и ∠К=90° , тк. опирается на диаметр MN , значит ∠N=90°⇒ противоположные стороны равны , т.е. проекция РН=NK.

По т. об углах с соответственно перпендикулярными сторонами ∠АВС=∠NMK ⇒ хорды АС=NK. Значит РН=АС

================================

Теорема об углах с соответственно перпендикулярными сторонами "Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180."