Предмет: Геометрия,
автор: ПолинаМаксименко
Помогите пожалуйста с решением. Наглядная геометрия 7 класс
Приложения:
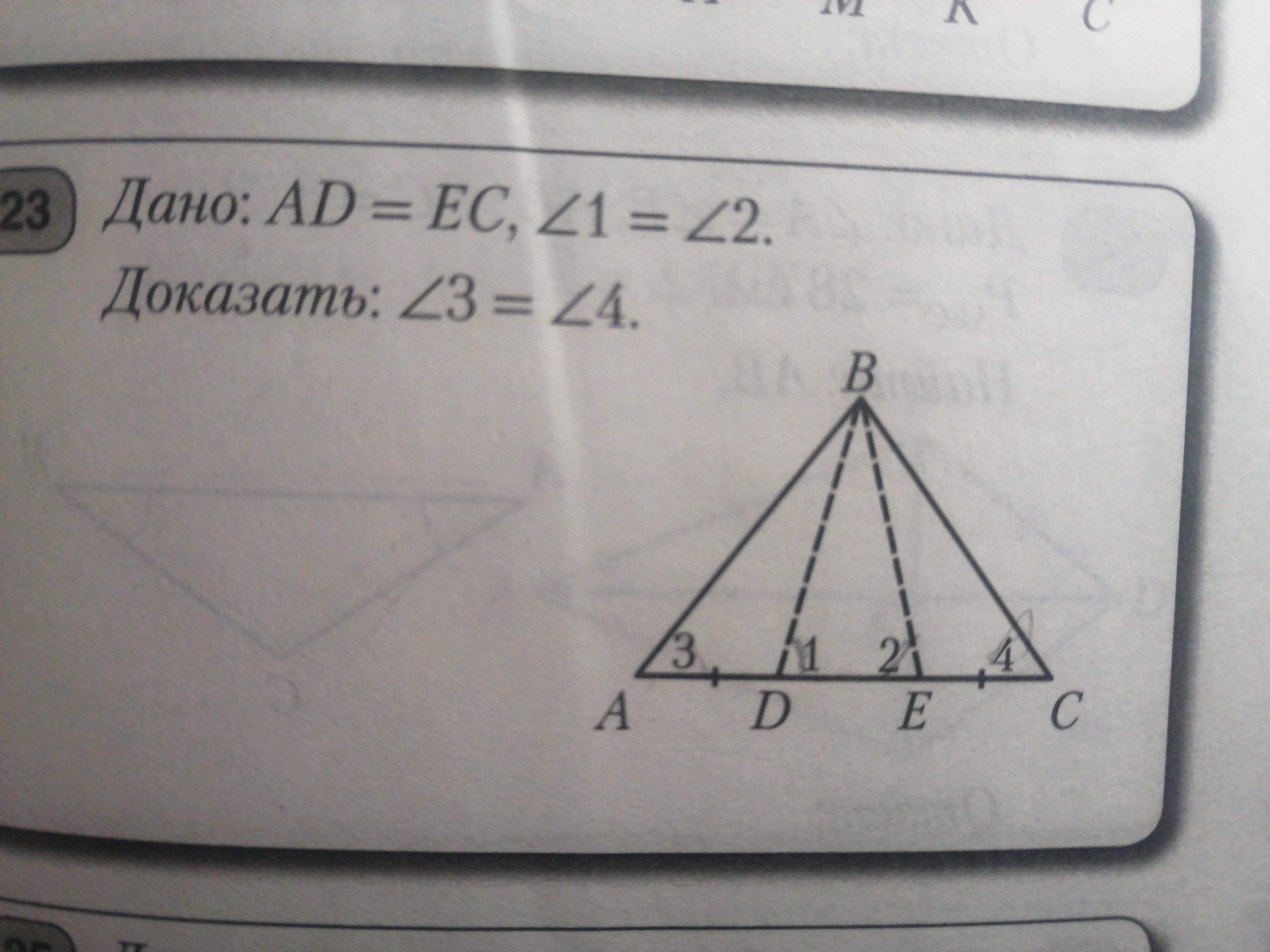
то есть что треугольники ABD=BEC
∆АВД=∆ЕВС. В ∆ДЕВ. <ВДЕ=<ВЕД по условию, значит ∆ ДЕВ равнобедренный, отсюда следует что ВД=ВЕ. Дальше. <АДЕ=180°развернутый. <АДВ=180-<1; <ДЕС=180° развернутый. <ВЕС=180°-<2, так как <1=<2, то <АДВ=<ДЕС. ∆ВАД=∆ВЕС по первому признаку две стороны и угол между ними.
Ответы
Автор ответа:
1
Угол 1 равен углу 2 следовательно треугольник DBE равнобедренный.
Угол BDA= углу ВЕС, АD=EC, BD=BE следовательно треугольники BAD и BEC равны по двум сторонам и углу между ними следовательно угол 3= углу 4 как соответственные элементы равных треугольников
Угол BDA= углу ВЕС, АD=EC, BD=BE следовательно треугольники BAD и BEC равны по двум сторонам и углу между ними следовательно угол 3= углу 4 как соответственные элементы равных треугольников
Похожие вопросы
Предмет: Английский язык,
автор: 5Roner5
Предмет: Русский язык,
автор: moragames1
Предмет: Русский язык,
автор: Nikita01111
Предмет: Алгебра,
автор: Lolkslol
Предмет: Математика,
автор: tanya27081
1. АD=EC ( по условию).
2. угол 1 равен углу 2 соответственно угол ADB=BEC.
3. АС общая .
с последним не уверенна