Предмет: Алгебра,
автор: nachaloclashofclans1
помогите пж алгебра9 класс
Приложения:
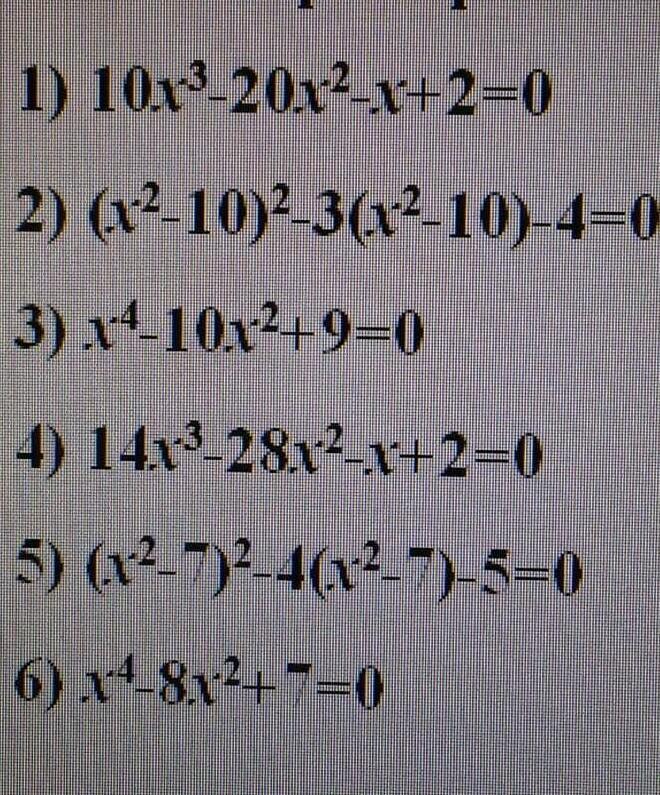
Ответы
Автор ответа:
0
Ответ:
Объяснение:
1)
Решим группировкой
ответ: 2;
2)Решим заменой => x^2-10=t
a)
б)
Ответ: 3 ; -3 ;
3) Замена x^2=y
x= { ±1;±3}
Ответ: 1 ; -1 ; 3 ; -3
4)Группировка
x=±
Ответ: 2 ; ; -
5) замена x^2-7=t
а)
б)
Ответ:
6) x^2=y
x={± ; ±1}
Ответ : 1 ; -1 ;
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: simanovic60
Предмет: Русский язык,
автор: khaspalaeva04
Предмет: Математика,
автор: VladislavAkinshin