Предмет: Математика,
автор: lemurity
Найти производную функции
Приложения:
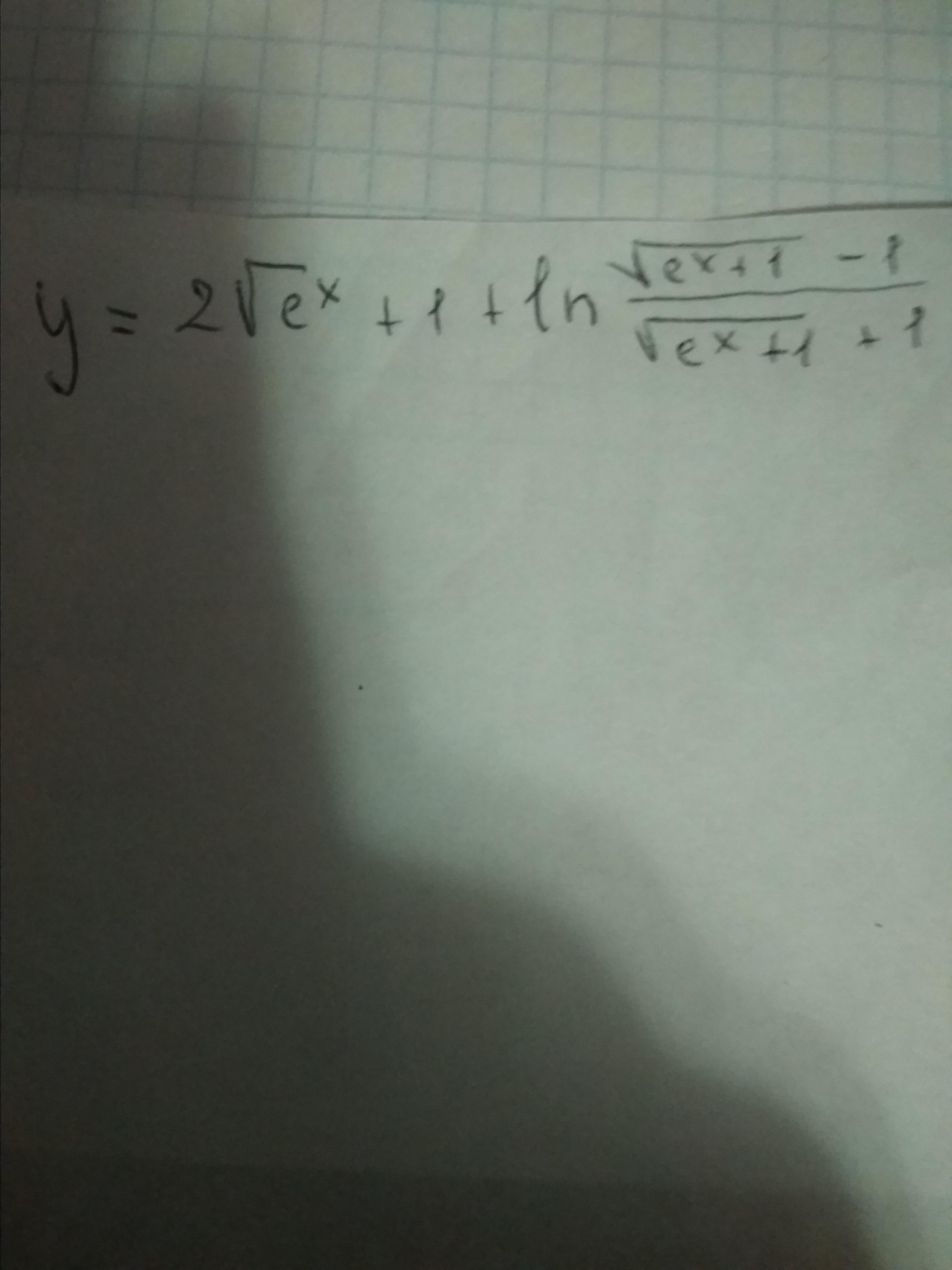
Ответы
Автор ответа:
1
Ответ:
решение на фотографии
Приложения:
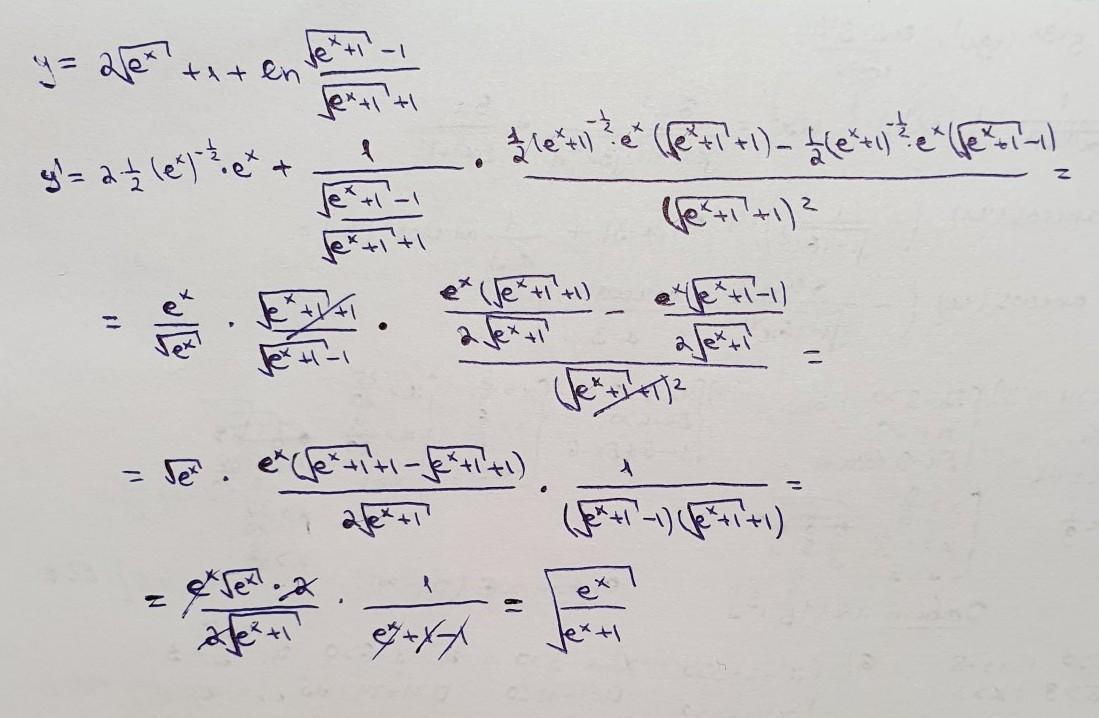
NNNLLL54:
в 3 строке вместо (+) поставили (*) ...
Спасибо!
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: aitan23051995
Предмет: Английский язык,
автор: samalahka55
Предмет: Українська мова,
автор: iiiim
Предмет: Математика,
автор: nataly77782oy331z