Предмет: Математика,
автор: vgorskova040
Помогите, желательно с объяснением) даю 50 баллов. Нужно решить и найти область определения
Приложения:
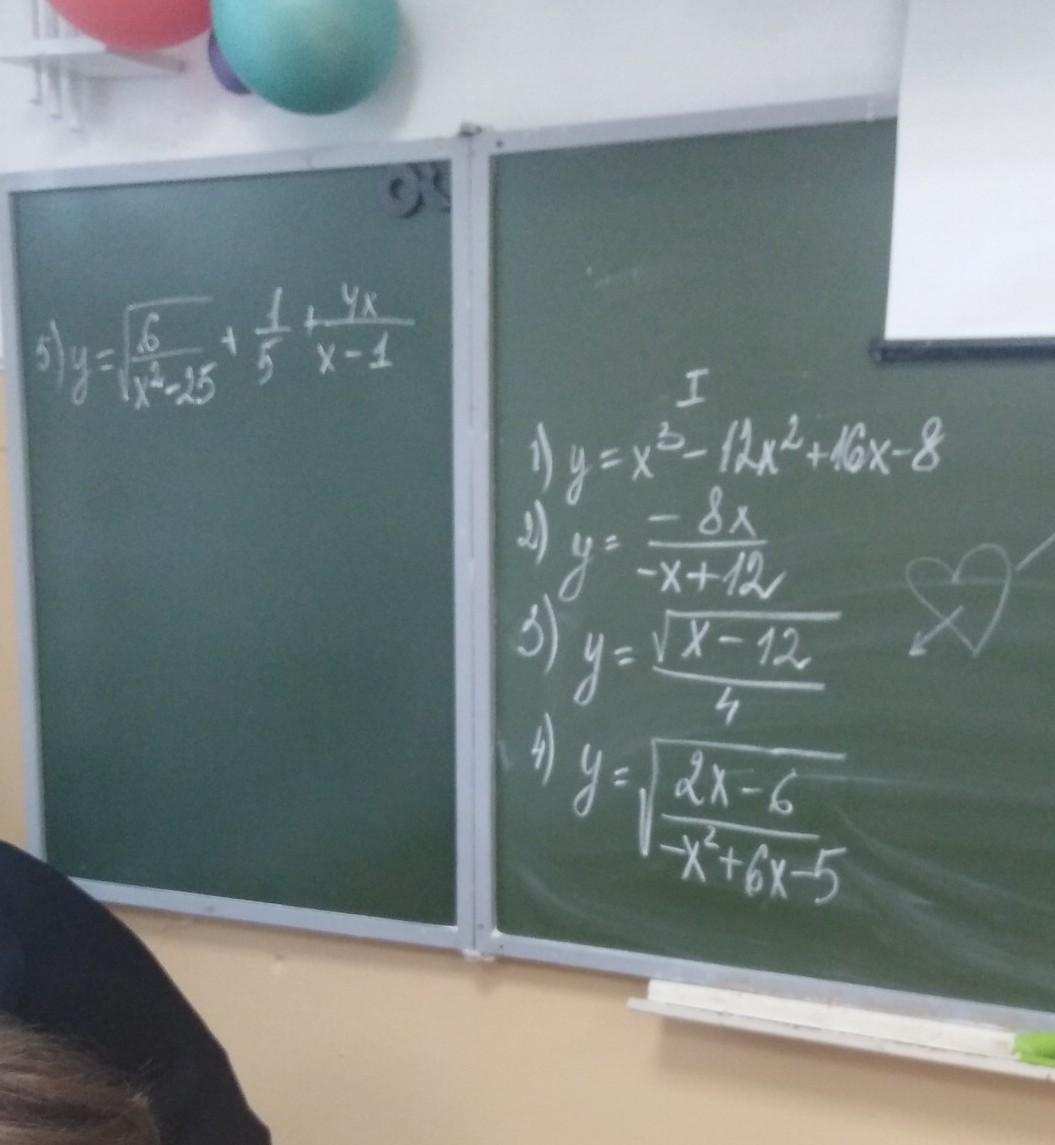
vgorskova040:
первый
ну значит 3
2,3,4
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1)y=-8 x∈R
2)x∈R/(12)
3)нет пересечений с осью y x∈|12;+∞)
4)y=√30/5 x∈(-∞;1)∪|3;5)
5) нет пересечений с осью y x∈(-∞;-5)∪(5;+∞)
Автор ответа:
1
Ответ:
↓↓↓↓
Пошаговое объяснение:
2.у= здесь знаменатель не должен равнятся 0ю
-х+12≠0 ⇒х≠12. Область определения х любое кроме 0
3.у= в знаменателе конкретное число без х. значит это не опасно. Но есть корень и тогда х-12≥0 ,х≥12 .Область определения х≥12.
4.у= ну здесь сплошные заморочки и корень и дробь!
-х²+6х-5=0 , Д=36-20=16 , х1=1, х2=-10.
по м. интервалов. не завыть кружочки знаменателя пустые!!!
+ - + -
______(-10)____(1)_____[3]_______
Область определения х<-10, 1<x≤3.
Похожие вопросы
Предмет: Русский язык,
автор: 86gka
Предмет: Английский язык,
автор: nellicoala
Предмет: Русский язык,
автор: Veronika49256
Предмет: Биология,
автор: dmrnk
Предмет: Математика,
автор: иринка244